Examples for recrystallization and grain growth simulations

The paper introduces a scalable three dimensional (3D) kinetic cellular
automaton model with a probabilistic switching rule for the patial and crystallographic prediction of mesoscale transformation phenonomena that involve orientational field variables and the motion of sharp interfaces such as
encountered in the field of recrystallization. The automaton is discrete in time,
physical space and Euler orientation space. It is defined on a regular 3D cubic 
lattice considering the first-, second- and third-neighbour shells for the calculation of the local driving forces. 

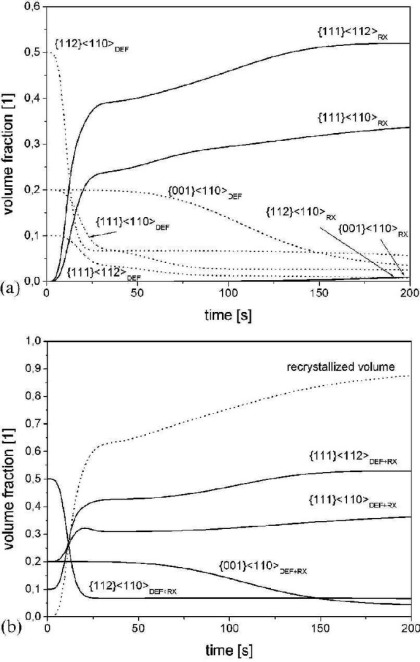
This paper discusses the most relevant multiscale models for predicting crystallographic textures formed during the primary static recrystallization of metals. Two main groups of approaches are presented, namely those which spatially discretize the grains and the interface motion associated with recrystallization and those which treat these phenomena in an Avrami-type statistical fashion. The article gives a concise review of the methods, placing
particular attention on their strengths and weaknesses in the context of process modelling, of conceptual aspects, and of the data sets required as input for practically applying the models to the prediction of crystallographic textures in the course of metallurgical processes.

The paper is about cellular automaton models in materials science. It
gives an introduction to the fundamentals of cellular automata and reviews applications, particularly for those that predict recrystallization phenomena. Cellular automata for recrystallization are typically discrete in time, physical space, and orientation space and often use quantities such as dislocation density and crystal orientation as state variables. Cellular automata can be defined on a regular or nonregular two- or three-dimensional lattice considering the first, second, and third neighbor shell for the calculation of
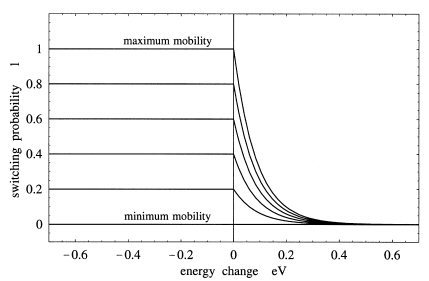
the local driving forces. The kinetic transformation rules are usually formulated to map a linearized symmetric rate equation for sharp grain boundary segment motion. While deterministic cellular automata directly perform cell switches by sweeping the corresponding set of neighbor cells in accord with the underlying rate equation, probabilistic cellular automata calculate the switching probability of each lattice point and make the actual decision about a switching event by evaluating the local switching probability using a Monte Carlo step. Switches are in a cellular automaton algorithm generally performed as a function of the previous state of a lattice point and the state of the neighboring lattice points. The transformation rules can be scaled in terms of time and space using, for instance, the ratio of the local and the maximum possible grain boundary mobility, the local crystallographic texture, the ratio of the local and the maximum-occurring driving forces, or appropriate scaling measures derived from a real initial specimen. The cell state update in a cellular automaton is made in synchrony for all cells. The review deals, in particular, with the prediction of the kinetics, microstructure, and texture of recrystallization. Couplings between cellular automata and crystal plasticity finite element models are also discussed.

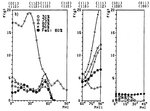
The concurrent ferrite recrystallization and austenitic transformation during intercritical annealing of cold-rolled DP steels is investigated by cellular automaton (CA) modeling. The simulations provide insight into the microstructural phenomena that result from the interaction of primary recrystallization and phase transformation. We find that the interaction between ferrite recrystallization and austenite formation affects not only the transformation kinetics but also the morphology and spatial distribution of the austenite. From this we can interpret experimental data of the observed temperature-dependent hardness and its dependence on the two metallurgical processes. The influence of the initial heating rate on subsequent isothermal transformation kinetics and the microstructure evolution is also obtained by the model.

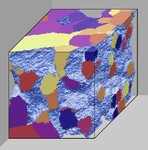
The paper presents a two-dimensional approach for simulating primary static
recrystallization, which is based on coupling a viscoplastic crystal plasticity finite-element model with a probabilistic kinetic cellular automaton. The crystal plasticity finite-element model accounts for crystallographic slip and for the rotation of the crystal lattice during plastic deformation. The model uses space and time as independent variables and the crystal orientation and the accumulated slip as dependent variables. The ambiguity in the selection of the active slip systems is avoided by using a viscoplastic formulation that assumes that the slip rate on a slip system is related to the resolved shear stress through a power-law relation. The equations are cast in an updated Lagrangian framework. The model has been implemented as a user subroutine in the commercial finite-element code Abaqus. The cellular automaton uses a switching rule that is formulated as a probabilistic analogue of the linearized symmetric Turnbull kinetic equation for the motion of sharp grain boundaries. The actual decision about a switching event is made using a simple sampling
nonMetropolis Monte Carlo step. The automaton uses space and time as independent variables and the crystal orientation and a stored energy measure as dependent variables. The kinetics produced by the switching algorithm are scaled through the mesh size, the grain boundary mobility, and the driving force data. The coupling of the two models is realized by: translating the state  variables used in the finite-element plasticity model into state variables used in the cellular automaton; mapping the finite-element integration point locations on the quadratic cellular automaton mesh; using the resulting cell size, maximum driving force, and maximum grain boundary mobility occurring in
the region for determining the length scale, time step, and local switching probabilities in the automaton; and identifying an appropriate nucleation criterion. The coupling method is applied to the two-dimensional simulation of texture and microstructure evolution in a heterogeneously deformed, high-purity aluminium polycrystal during static primary recrystallization, considering
local grain boundary mobilities and driving forces.

A method is introduced for scaling Monte Carlo kinetics of the Potts model using rate theory. The method is particularly designed for the kinetic and spatial scaling of multistate kinetic Potts models using one or more sets of non-conserved structural or orientational state variables Si each of which can
assume a number of Qi degenerate ground states (Q or multistate Potts models) as commonly employed for simulating recrystallization and curvature driven grain growth phenomena. The approach is based on the equivalence of single-site state switches in the Potts model and grain boundary motion as described by Turnbull's classical rate theory mapped on a simulation lattice. According to this approach the switching probabilities can be scaled by the ratio of the local and the maximum occurring values of the grain bound-
ary mobility and by the ratio of the local and the maximum occurring values of configurational and scalar contributions to the driving force. The real time step elapsing during one Monte Carlo time step is scaled by the maximum occurring grain boundary mobility, the maximum occurring driving force, and the lattice
parameter of the simulation grid. 

A brief summary of simulation techniques for recrystallization is given. The limitations of the Potts model and the cellular automaton model as used in their standard forms for grain growth and recrystallization are noted. A new approach based on a hybrid of the Potts model (Me) and the cellular automaton (CA) model is proposed in order to obtain the desired limiting behavior for both curvaturc-driven and stored cncrgy-driven grain boundary migration.

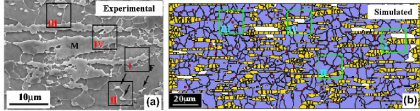
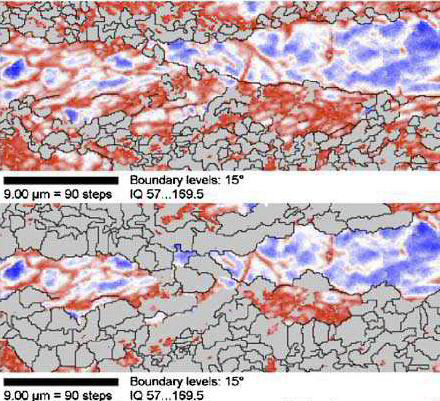
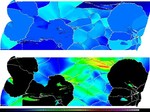
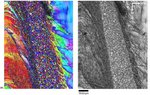
This is a 2D cellular automaton simulation study on the evolution of the recrystallization texture in a 75% cold rolled interstitial free (IF) sheet steel. The model is applied to experimentally obtained high resolution microtexture EBSD
data. The simulation is discrete in time and physical space. Orientation is treated as a continuous variable in Euler space. The dislocation density distribution is approximated from the Kikuchi pattern quality of the experimental EBSD
data. It is used for the calculation of the scalar driving force field required for the recrystallization simulation. Different models for nucleation and for the influence of Zener-type particle pinning are presented and tested. Real time and space
calibration of the simulation is obtained by using experimental input data for the grain boundary mobility, the driving
forces, and the length scale of the deformed microstructure as mapped by the high resolution EBSD experiments. The simulations predict the kinetics and the evolution of microstructure and texture during recrystallization. Depending on
the ratio of the precipitated volume fraction and the average radius of the particles the simulations reveal three different regimes for the influence of particle pinning on the resulting microstructures, kinetics and crystallographic textures.