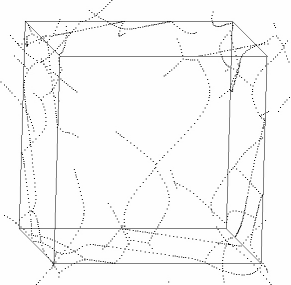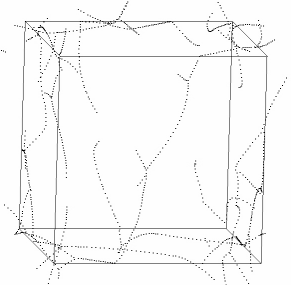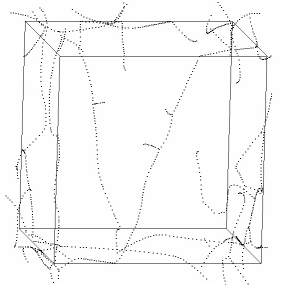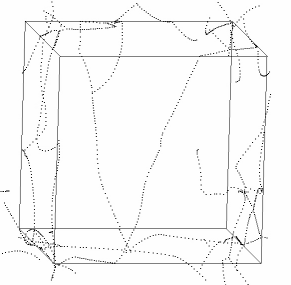
DDD: Discrete Dislocation Dynamics
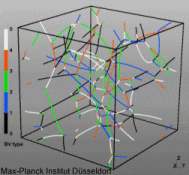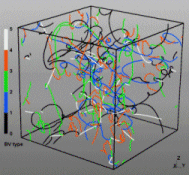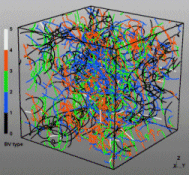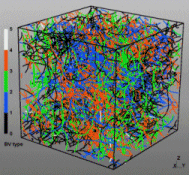
Discrete dislocation dynamics simulations (DD or DDD) average out the atomistic nature of the material by reducing the direct atomic interactions to linear continuum elasticity. They calculate the exact positions and velocities of all dislocation segments at each instant. Three-dimensional discrete dislocation dynamics models simulate dislocation motion and multiplication in response to external loading, dislocation interactions (material strength) and track topology evolution of dislocation networks (microstructure). Numerical simulations with these models have profoundly assisted progress in dislocation physics.
In our work we mainly use a modified version of the ParaDiS code (DD code developed at Lawrence Livermore National Laboratory). This approach simulates a dislocation network represented by a set of nodes connected by line segments. One stable dislocation node connects a maximum of four segments (arms). Each segment carries a Burgers vector and is assigned a glide plane normal. The conservation of the Burgers vector is assured everywhere in the dislocation network, except at a pinned node with a single arm (e.g. the end points of a Frank–Read source).
The force on a dislocation node due to the stress field of its own arms and other segments in the system is calculated based on a non-singular self-consistent stress field
formulation. The nodal force exerted by external loading is calculated through the Peach-Koehler equation. The nodal velocity is proportional to the projected nodal force by a
mobility tensor. The topology update of a dislocation network reflects the physics of dislocation motion and collisions in real crystals: Burgers vector reactions (annihilation, junction zipping and
unzipping) happen naturally through the collisions and dissociations of dislocation nodes.
Raabe_dislocation_dynamics_basics-short-[...]
PDF-Dokument [1.0 MB]
J.-l. Zhang,S.Zaefferer, D.Raabe
Materials Science & Engineering A 636 (2015) 231-242
A study on the geometry of dislocation patterns in the surrounding of nanoindents in a TWIP steel using electron channeling contrast imaging and discrete dislocation dynamics simulations
Materials Science Engin A636 (2015) 231 [...]
PDF-Dokument [1.5 MB]
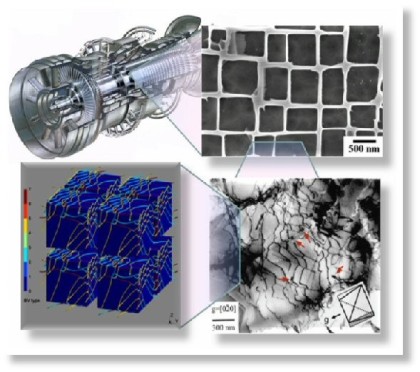
Electron channeling contrast imaging under controlled diffraction conditions (cECCI) enables observation of crystal defects, especially dislocations, stacking faults and nano-twins, close to the surface of bulk samples. In this work cECCI has been employed to observe defects around nanoindents into the surface of {100}-, {110}-, {111}-oriented grains in a Fe–22Mn–0.65C (wt%) TWIP steel sample (fcc crystal structure, stacking fault energy 20 mJ/m²) using a cone-spherical indenter. The dislocation patterns show four- and two-fold symmetries for the {100}- and {110}-orientation, and a three-fold symmetry for the {111}-orientation which is, however, difficult to observe. Discrete dislocation dynamics (DDD) simulations of the indentation were carried out to complement the static experimental investigations. The simulations were carried out with both, cross-slip disabled and enabled conditions, where the former were found to match to the experimental results better, as may be expected for an fcc material with low stacking fault energy. The 3-dimensional geometry of the dislocation patterns of the different indents was analysed and discussed with respect to pattern formation mechanisms. The force– displacement curves obtained during indentation showed a stronger strain hardening for the {111} oriented crystal than that for the other orientations. This is in contrast to the behaviour of, for example, copper and is interpreted to be due to planar slip. Irrespective of orientation and indentation depth the radius of the plastically deformed area was found to be approximately 4 times larger than that of the indenter contact area.
For the discrete dislocation simulations we used the ParaDiS code which was developed at Lawrence Livermore National Laboratory [21]. The method represents a dislocation network in terms of an array of interconnected nodes which have line segments between them. One single stable dislocation node can
connect up to four individual segments (dislocation arms). Each of the dislocation segments carries a Burgers vector and is assigned a glide plane normal. The Burgers vector is conserved
everywhere in a dislocation network, except for the case of a pinned node with a single arm, such as for instance encountered at the end points of a Frank–Read source. The resulting
force exerted on a specific dislocation node due to the elastic stress field exerted by its own dislocation arms and by the elastic stresses of all other dislocation
segments in the system is calculated using a non-singular elastic formulation suggested by Cai et al. [27]. The additional nodal force created by the external loading conditions is
calculated by using the Peach–Koehler equation. The resulting nodal velocity is proportional to the projected nodal force through a mobility tensor which essentially differentiates
between glide and climb. The
topology update of such a loaded dislocation network mimics all relevant motion and collision phenomena that are potentially encountered in a real crystal. Reactions such as
annihilation, junction zipping as well as junction unzipping occur through the collisions and dissociations of dislocation nodes [21].
For simulating the current indentation experiments a sample box geometry of 12,000 b!12,000 b!1600 b (b being the length of the Burgers vector) was chosen. 5000 time steps were used
for loading, 5000 for holding, and 5000 for unloading. The simulations were conducted for crystal orientations [001], [011], and [111]. In order to elucidate the effect of the
relatively low stacking fault energy of the material under investigation the simulations were carried out using the related elastic parameters of pure Cu. Simulations were conducted
using both, cross-slip disabled and enabled conditions in order to study the effect of the stacking fault energy on the resulting dislocation pattern formation. In accordance
with the experimental observations no mechanical twinning was enabled in the simulations.
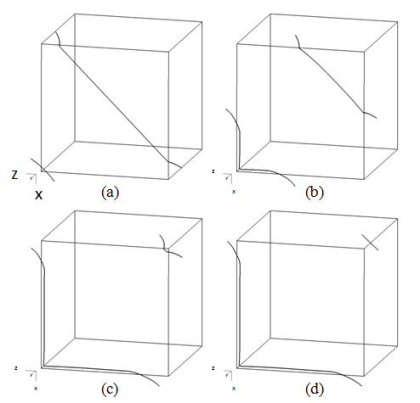
The transmission of an incoming dislocation through a symmetrical low-angle tilt grain boundary (GB) is studied for {110}<111> slip systems in body-centered cubic metals using discrete dislocation dyn
Acta-Mater-2011-dislocation-wall-DDD.pdf
PDF-Dokument [3.0 MB]
Acta Materialia 60 (2012) 5380-5390
Simulation of dislocation penetration through a general low-angle grain boundary
B. Liu, P. Eisenlohr, F. Roters, D. Raabe
Acta-Materialia-Dislocation-network-pene[...]
PDF-Dokument [3.3 MB]
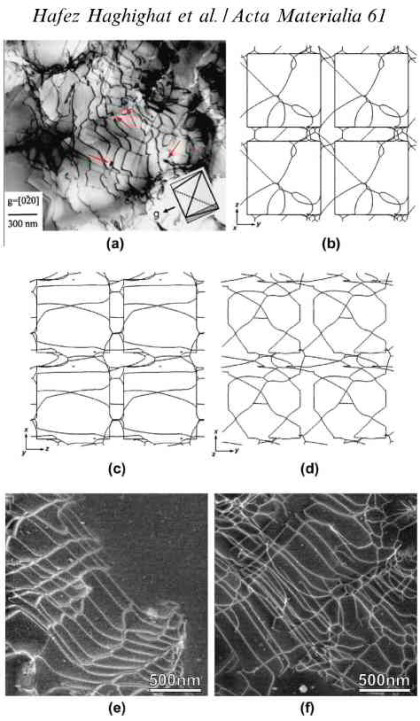
The development of the dislocation structure in crystalline solids (having either face-centered cubic, body-centered cubic or hexagonal lattices) follows a universal evolution when starting from a
state of low dislocation content up to large strains. The various structural components reach a dynamically equilibrated state after different amounts of strain. The most rapid development is
the increase in content of free dislocations, which scales with flow stress. A concurrent but slower development is the growing density of low-angle grain boundaries (LAGBs) that accommodate the
fragmentation of the crystallites. Such fragmentation is inevitable because of spatially heterogeneous boundary conditions resulting from, for instance, variability in operable slip systems or
grain neighborhood. The average disorientation across LAGBs increases at an even lower rate and, after severe plastic deformation, ultimately transforms the subgranular structure into a high-angle
grain boundary (HAGB)-dominated polycrystal. At this stage, the spacing of HAGBs is closely related to the previously established LAGB spacing, which is found to scale (approximately) in inverse
proportion to the saturation stress. The overall structural refinement entails a marked increase in deformation resistance, the majority of which is correlated to the increase in the LAGB
density.
In order to capture the influence of LAGBs on strength and strain hardening in crystal plasticity, a fundamental understanding of their role is required. Comparable basic insights into materials
strengthening have been provided by recent molecular dynamics (MD) and discrete dislocation dynamics (DDD) simulations of dislocation interactions (MD & DDD), irradiation-induced hardening (MD
& DDD), thin metal and semiconductor films (DDD), microscale size-dependent strengthening (DDD), nanocrystalline metals (MD) and nanoscale twin boundary strengthening (MD).
The present work focuses on the ability of dislocations to penetrate general low-angle (coherent) grain boundaries.
Penetration resistance has long been expected to be dominated by the local interaction between the incident and LAGB dislocations. Given the strong dislocation interactions, particularly collinear
annihilation and ternary junctions that can occur between incident and network dislocations, it is reasonable to believe that such a LAGB can make a substantial contribution to material
strength.
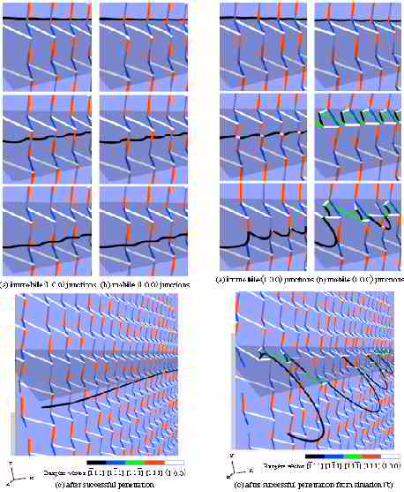
The present paper studies the transmission of incident lattice dislocations through a LAGB using DDD simulations. The body-centered cubic (bcc) lattice structure is chosen primarily to avoid
implementation difficulties associated with planar dislocation dissociation. A general LAGB is composed of two or more sets of mixed dislocations. We idealize such a LAGB as a perfect regular
mesh constructed from two sets of dislocations that relax into a hexagonal network by formation of h100i binary junctions. Assuming on average equal slip activity on all three possible slip system
pairs that form binary junctions, networks containing the most stable mixed-symmetrical binary junction would then be the most likely ones to occur. The following aspects will be studied: (1)
comparison of the transmission stresses for three incident dislocation types that undergo different reactions with the dislocation network; (2) dependence of transmission stress on the mobility of
h100i dislocations; (3) dislocation processes occurring during network penetration.
We use a modified version of the ParaDiS DDD code (developed at Lawrence Livermore National Laboratory). The modification we have introduced consists of uncoupling the crystal and laboratory
coordinate systems in order to be able to solve the dislocation–LAGB interaction problem in various laboratory frames. The laboratory coordinate systems for the subsequent simulations are
chosen such that (i) the X-axis coincides with the LAGB plane normal, (ii) the Z-axis runs along the intersection line between the incident slip plane and the LAGB plane, and (iii) the Y-axis follows
as the cross-product of the first two axes. A cubic simulation box with edge length of 7200b (7200 times the magnitude of the Burgers vector) is used, which is periodically extended in the X, Y and Z
directions.
Dierk Raabe Superalloys Royal Socoety Ch[...]
PDF-Dokument [3.1 MB]
Discrete dislcoation dynamics for the simulation of creep in superalloys
Creep of single-crystal superalloys is governed by dislocation glide, climb, reactions and annihilation. Discrete three-dimensional (3D) dislocation dynamics (DDD) simulations are used to study the evolution of the dislocation substructure in a gamma/gamma' microstructure of a single-crystal superalloy for different climb rates and loading conditions. A hybrid mobility law for glide and climb is used to map the interactions of dislocations with gamma'cubes. The focus is on the early stages of creep, where dislocation plasticity is confined to narrow gamma channels. With enhancing climb mobility, the creep strain increases, even if the applied resolved shear stress is below the critical stress required for squeezing dislocations into the gamma channels. The simulated creep microstructure consists of long dislocations and a network near the corners of the c0 precipitate in the low-stress regime. In the high-stress regime, dislocations squeeze into the c channels, where they deposit dislocation segments at the gamma/gamma'interfaces. These observations are in good agreement with experimentally observed dislocation structures that form during high-temperature and low-stress creep.
discrete-dislocation-modeling-superalloy[...]
PDF-Dokument [2.9 MB]
Creep of single-crystal superalloys is governed by dislocation glide, climb, reactions and annihilation. Discrete three-dimensional (3D) dislocation dynamics (DDD) simulations are used to
study the evolution of the dislocation substructure in a gamma/gamma' microstructure of a single-crystal superalloy for different climb rates and loading conditions. A hybrid mobility law
for glide and climb is used to map the interactions of dislocations with gamma' cubes. The focus is on the early stages of creep, where dislocation plasticity is confined to
narrow gamma channels. With enhancing climb mobility, the creep strain increases, even if the applied resolved shear stress is below the critical stress
required for squeezing dislocations into the c channels. The simulated creep microstructure consists of long dislocations and a network near the corners of the gamma' precipitate in the
low-stress regime. In the high-stress regime, dislocations squeeze into the c channels, where they deposit dislocation segments at the gamma/gamma' interfaces. These observations are in
good agreement with experimentally observed dislocation structures that form during high-temperature and low-stress creep.
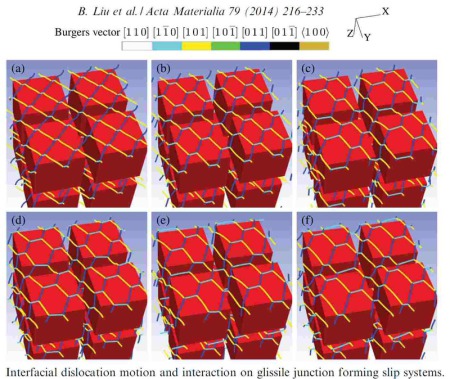
Acta Materialia 79 (2014) 216-233
Using recent developments of discrete dislocation dynamics models, we simulate interfacial dislocation motion in the channel structures of single-crystal superalloys, and investigate how interfacial dislocation motion and dynamic recovery are affected by interfacial dislocation interactions and lattice misfit.
Acta Mater 2014 dislocations dynamics re[...]
PDF-Dokument [1.1 MB]
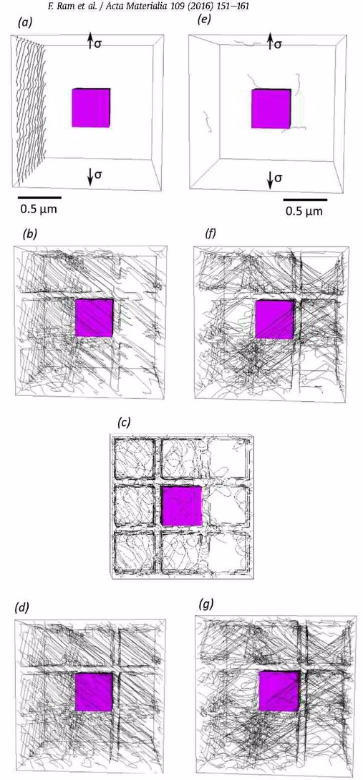
Acta Materialia 109 (2016) 151-161
Ram et al Ni base superalloy creep dislc[...]
PDF-Dokument [2.2 MB]
This work investigates the origin of creep dislocations in a Ni-base, single crystal superalloy subject to creep at an intermediate stress and temperature. Employing high angular resolution electron backscatter diffraction (HR-EBSD), electron channeling contrast imaging under controlled diffraction conditions (cECCI) and discrete dislocation dynamics (DDD) modelling, it is shown that low-angle boundaries—which correspond to dendrite boundaries or their residues after annealing—are not the major sources of creep dislocations. At the onset of creep deformation, they are the only active sources. Creep dislocations are emitted from them and percolate into the dislocation-depleted crystal. However, the percolation is very slow. As creep deformation proceeds, before the boundary-originated dislocations move further than a few micrometers away from their source boundary, individual dislocations that are spread throughout the undeformed microstructure become active and emit avalanches of creep dislocations in boundary-free regions, i.e. regions farther than a few micrometer away from boundaries. Upon their activation, the density of creep dislocations in boundary-free regions soars by two orders of magnitude; and the entire microstructure becomes deluged with creep dislocations. The total area of boundary-free regions is several times the total area of regions covered by boundary-originated creep dislocations. Therefore, the main sources of creep dislocations are not low-angle boundaries but individual, isolated dislocations in boundary-free regions