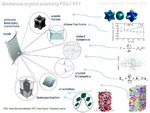
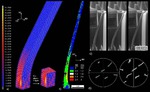
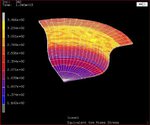
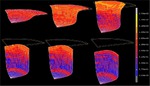
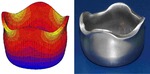
Advanced polycrystal mechanical modeling: The Crystal Plasticity Finite Element Simulation Method (CPFEM)
Polycrystal mechanics deals with the ansiotropic constitutive laws of the elastic-plastic deformation of crystals and their interactions among each other.
Reprints - single crystal and polycrystal mechanics
Applications of DAMASK to the Multi-Physics Crystal Plasticity and Damage Simulation of DP Steels
2018 Raabe 18th Intern Con on Strength o[...]
PDF-Dokument [7.6 MB]
Kuo et al.
Advanced Engineering Materials
Bicrystal Mechanics vol 5 (2003) page 563
Advanced Engin Mater bicrystal mechanics[...]
PDF-Dokument [174.7 KB]
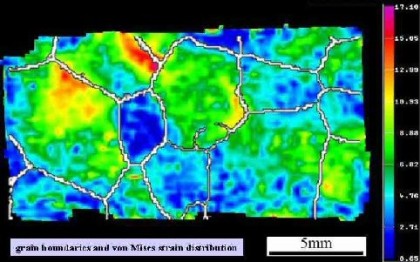
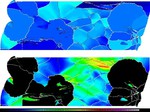
Grain boundaries are natural obstacles to the motion of dislocations during plastic straining of crystalline matter. As such, they may be the cause of grain-scale heterogeneity in terms of the mismatch of the elastic-plastic strain rate, internal stress, and crystallographic reorientation rate fields. Investigating such non-homogeneity systematically as a function of the grain boundary character under well-defined mechanical boundary conditions is important for a better understanding of grain-scale and grain-boundary micromechanics as well as the development of the micro- and nanoscale texture.
Together with my group at the Max-Planck Institut in Düsseldorf (http://www.mpie.de)
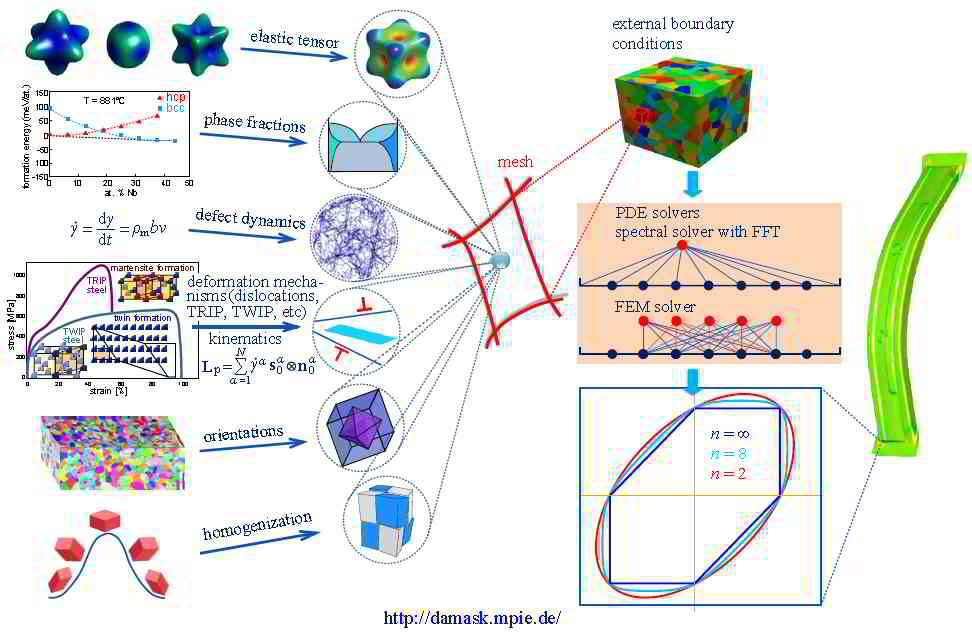
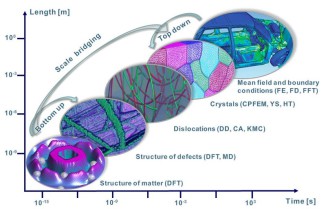
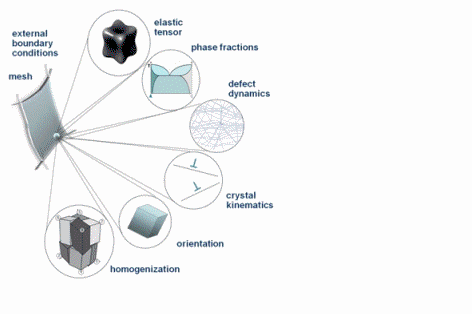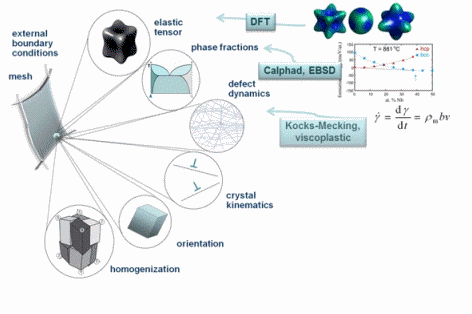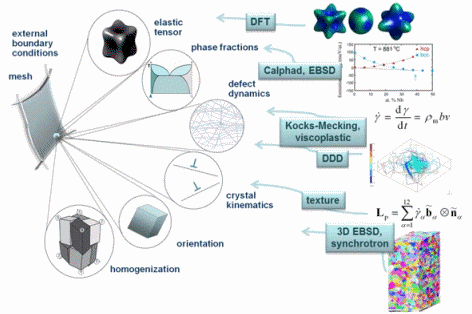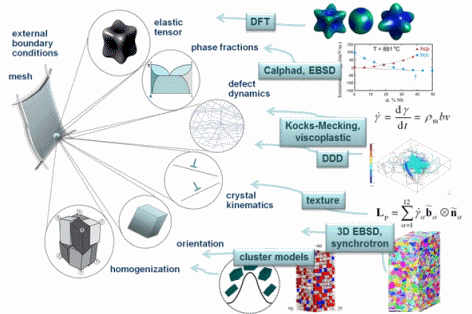
I am interested in the development of physically-based crystal plasticity constitutive models for describing and understanding the micromechanical behaviour of crystalline materials. The models are based on rate formulations that describe the evolution of lattice defects under external loads. The constitutive rate formulations account for the crystalline nature of the material, i.e. they describe lattice defect kinetics individually on all crystallographic shear and slip systems. This approach renders the constitutive models anisotropic. The formulations are built on mobile, sessile, and geometrically necessary dislocation populations, and on mechanical twinning as underlying deformation carriers. The resulting lattice defect density quantities are used in kinematic state equations for the calculation of the local and global stresses. The mechanics at grain boundaries and heterophase interfaces are also addressed. Standard nonlinear Finite Element solvers (FEM) are used for solving the coupled sets of partial differential equations rendering the approach an internal-variable based crystal plasticity finite element method (CPFEM). Recently, particular attention has been placed on developing multi-scale crystal plasticity finite element and Fast Fourier simulations. Three directions are pursued in this context. The first approach lies in an increasing interest to consider the (tensorial) stress fields of single dislocations in crystal plasticity constitutive models. In some cases such as Bauschinger phenonena (flow stress changes upon load reversal) the effect of the tensor stress field of individual dislocations seems to play an important role for micro- and nanoscale deformation problems. The second field concerns the direct use ab initio simulation results in crystal plasticity finite element simulations. Typical examples are the use of phase fractions and / or elastic constants that cannot be obtained by experiment as input parameters in crystal mechanical simulations.The third direction is the connection between discrete dislocation dynamical models (DDD) and the crystal plasticity finite element method.
Acta Materialia 80 (2014) 77-93
Acta Materialia 2014 Sandlobes Mg rare e[...]
PDF-Dokument [1.1 MB]
The microstructure evolution of pure Mg and two Mg–rare-earth alloys (Mg–3 wt.% Dy and Mg–3 wt.% Er) was studied during in situ compression tests by electron backscatter diffraction and
electron channelling contrast imaging. Strain localization and the formation of an early stage shear band (“pre-shear band”) were observed in pure Mg during compressive deformation below 5%
engineering strain. In the experiments percolative grain clusters with prevalent basal slip as a precursor for shear band formation was observed. This
collective grain-cluster shear behaviour was analysed in more detail using crystal plasticity simulations, revealing a percolation of intense basal slip activity across grain boundaries as the
mechanism for shear band initiation. Plane trace analysis, Schmid factor calculation and deformation transfer analysis at the grain boundaries were performed for the activated twins. It appears
that many activated tension twins exhibit pronounced non-Schmid behaviour. Twinning appears to be a process of accommodating local strain rather than a response to macroscopic strain.
Acta Materialia 91 (2015) 267-288
Acta Materialia 91 (2015) 267 Magnesium [...]
PDF-Dokument [2.1 MB]
We present the orientation dependent indentation response of pure magnesium during single grain indentation. A conical indenter and maximum loads between 50 mN and 900 mN were employed. Indent topographies were acquired by confocal microscopy. The indents were also characterized by electron backscatter orientation microscopy for their microstructures. Pronounced activation of specific twinning systems was observed around the impressions. The resulting data were compiled into the inverse pole figure presentation of indent microstructures and topographies after Zambaldi and Raabe, Acta Mater. (2010). Three-dimensional crystal plasticity finite element simulation of the indentation deformation supports the interpretation of the orientation dependent slip and twinning patterns around the indents. The match between the activation of observed and simulated twinning variants is discussed with respect to the conditions for nucleation and growth of extension twins. Furthermore, the compatibility of the twinning strains with the imposed deformation is discussed based on the expanding cavity model of indentation. The orientation dependent response of magnesium during indentation is compared to the literature data for indentation of alpha-titanium and beryllium. Recommendations are given on how to exploit the characteristic nature of the observed indentation patterns to rapidly assess the relative activity of deformation mechanisms and their critical shear stresses during alloy development.
Computational Materials Science 39 (2007) 91–95
A. Ma, F. Roters, D. Raabe
A dislocation density based constitutive law for BCC materials in crystal plasticity FEM
Computational Materials Science 39 (2007[...]
PDF-Dokument [1.0 MB]
We introduce a crystal plasticity constitutive model for BCC materials which is build on dislocation movement and uses dislocation density variables as internal state variables. Besides the statistically stored dislocations geometrically necessary dislocations are used to consider nonlocal effects as recently proposed by Ma, Roters and Raabe for the FCC crystal structure. In this paper the model will be adopted to the BCC crystal structure. Due to the special core structure of screw dislocations formed at low temperatures, the mechanical behavior of BCC crystals is controlled by the movement of screw dislocations rather than edge dislocations. For this reason, the Peierls mechanism has to be considered and several modifications have been introduced which include a new scaling relation between the mobile and immobile dislocations, and new flow rules for bulk and grain boundary elements. A pure Nb bicrystal is studied experimentally and numerically under channel die compression boundary conditions, to demonstrate the applicability of the new model variant.
Advanced Engineering Materials vol 4, pages 169-180 (2002)
D. Raabe, P. Klose, B. Engl, K. P. Imlau, F. Friedel, F. Roters
Advanced Engin Materials Raabe Klose ove[...]
PDF-Dokument [915.3 KB]
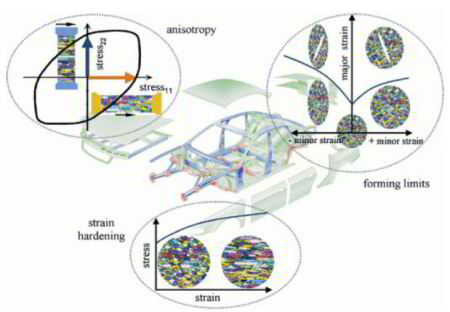
Modern metal forming and crash simulations are usually based on the finite element method. Aims of such simulations aye typically the prediction of the material shape, failure, and mechanical properties during deformation. Further goals lie in the computer assisted lay-out of manufacturing tools used for intricate processing steps. Any such simulation requires that the material under investigation is specified in terms of its respective constitutive behavior. Modern finite element simulations typically use three sets of material input data, covering hardening, forming limits, and anisotropy. This overview article is about the latter aspect. It reviews different empirical and physically based concepts for the integration of the elastic-plastic anisotropy into metal forming finite element simulations. Particular pronunciation is placed on the discussion of the crystallographic anisotropy of polycrystalline material rather than on aspects associated with topological or morphological microstructure anisotropy. The reviewed anisotropy concepts are empirical yield surface approximations, yield surface formulations based on crystallographic homogenization theory, combinations of finite element and homogenization approaches, the crystal plasticity finite element method, and the recently introduced texture component crystal plasticity finite element method. The paper presents the basic physical approaches behind the different methods and discusses engineering aspects such as scalability, flexibility, and texture update in the course of a forming simulation.
Int J Plast 24 (2008) 2278 grain mechani[...]
PDF-Dokument [2.7 MB]
International Journal of Plasticity 24 (2008) 2278-2297
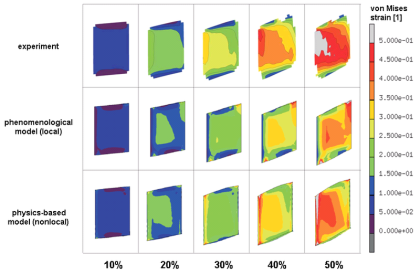
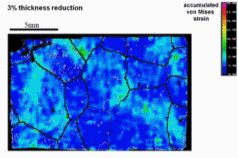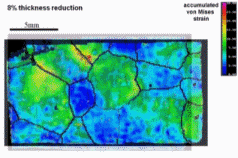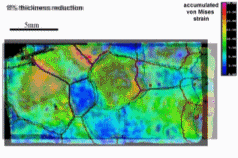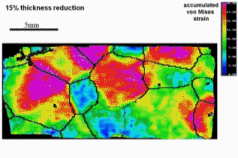
Here we study of plastic strain localization, surface roughening and of the origin of these phenomena in polycrystals. An oligocrystal aluminum sample with a single quasi-2D layer of
coarse grains is plastically deformed under uniaxial tensile loading. During deformation, the history of strain localization, surface roughening, microstructure and in-grain fragmentation
is carefully recorded. Using a crystal plasticity finite element model, corresponding high-resolution simulations are conducted. A series of comparisons identifying aspects of good and of
less good match between model predictions and experiments is presented. The study suggests that the grain topology and microtexture have a significant influence on the origin of strain
heterogeneity. Moreover, it suggests
that the final surface roughening profiles are related both to the macro strain localization and to the intra-grain interaction. Finally slip lines observed on the surface of the samples are
used to probe the activation of slip systems in detail. The study concludes with an assessment of the limitations of the crystal plasticity model.
Crystal-Plasticity-Overview_Acta Materia[...]
PDF-Dokument [8.3 MB]
Acta Materialia 58 (2010) 1152:
The elastic–plastic deformation of crystalline aggregates depends on the direction of loading, i.e. crystals are mechanically anisotropic. This phenomenon is due
to the anisotropy of the elastic tensor and to the orientation dependence of the activation of the crystallographic deformation mechanisms (dislocations,
twins, martensitic transformations). A consequence of crystalline anisotropy is that the associated mechanical phenomena such as shape change, crystallographic
texture, strength, strain hardening, deformation-induced surface roughening and damage are also orientation dependent. This is not a trivial statement as it implies that
mechanical parameters of crystalline matter are tensor quantities. An example is the uniaxial stress–strain curve, which is the most important mechanical measure in structural
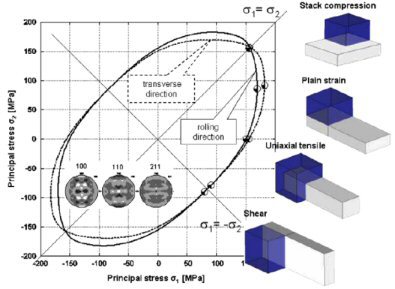
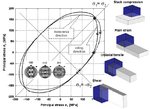
materials design. The statement above means that such flow curves represent an incomplete description of plastic deformation as they reduce a six-dimensional yield surface
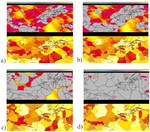
and its change upon loading to a one-dimensional (scalar) yield curve (see Fig. 1). Another consequence of this statement is that the crystallographic texture (orientation distribution) and its
evolution during forming is a quantity that is inherently connected with plasticity theory. Texture can hence be used to describe the integral anisotropy of polycrystals in terms of the individual
tensorial behavior of each grain and the orientation-dependent boundary conditions among the crystals. Formally, the connection between shear and texture evolution becomes clear from the fact that
any deformation gradient can be expressed as the combination of its skew-symmetric portion, which represents a pure rotation leading to texture changes if not matched by the rotation implied by
plastic shear, and a symmetric tensor that is a measure of pure stretching. Plastic shear hence creates both shape and orientation changes, except for certain highly symmetric shears. Therefore, a
theory of the mechanical properties of crystals must include, first, the crystallographic and anisotropic nature of those mechanisms that create shear, and second, the orientation(s) of the
crystal(s) studied relative to the applied boundary conditions (e.g. loading axis, rolling plane).
Early approaches to describe anisotropic plasticity under simple boundary conditions have considered these aspects, such as, for instance, the Sachs [3], Taylor [4],
Bishop-Hill [5,6] or Kröner [7] formulations. However, these approaches were neither designed for considering explicitly the mechanical interactions among the
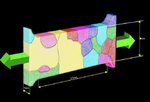
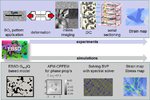
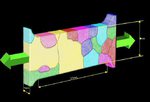
crystals in a polycrystal nor for responding to complex internal or external boundary conditions (Fig. 2). Instead, they are built on certain simplifying assumptions of strain or stress homogeneity
to cope with the intricate interactions within a polycrystal. For that reason variational methods in the form of finite-element (FE) approximations have gained enormous
momentum in this field. These methods, which are referred to as crystal plasticity finite-element (CPFE) models, are based on the variational solution of the equilibrium of the forces and the
compatibility of the displacements using a weak form of the principle of virtual work in a given finite-volume element. The entire sample volume under consideration is discretized into such
elements. The essential step which renders the deformation kinematics of this approach a crystal plasticity formulation is the fact that the velocity gradient is written in dyadic form. This
reflects the tensorial crystallographic nature of the underlying defects that lead to shear and consequently, to both shape changes (symmetric part) and lattice rotations
(skew-symmetric part)—see Section 3. This means that the CPFE method has evolved as an attempt to employ some of the extensive knowledge gained from experimental and theoretical studies of
single-crystal deformation and dislocations to inform the further development of continuum field theories of deformation. The general framework supplied by variational crystal plasticity
formulations provides an attractive vehicle for developing a comprehensive theory of plasticity that incorporates existing knowledge of the physics of deformation processes [8–10] into the
computational tools of continuum mechanics [11,12] with the aim of developing advanced and physically based design methods for engineering applications [13].
One main advantage of CPFE models lies in their ability to solve crystal mechanical problems under complicated internal and/or external boundary conditions. This aspect is not a mere
computational advantage but is an inherent part of the physics of crystal mechanics since it enables one to tackle those boundary conditions that are imposed by inter- and intra-grain micromechanical
interactions (see Fig. 3) [14]. This is not only essential to study in-grain or grain cluster mechanical problems but also to better understand the often quite abrupt mechanical transitions at
interfaces [15].
However, the success of CPFE methods is not only built on their efficiency in dealing with complicated boundary conditions. They also offer great flexibility with respect to including various
constitutive formulations for plastic flow and hardening at the elementary shear system level. The constitutive flow laws that were suggested during the last decades have gradually developed from
empirical viscoplastic formulations [16,17] into physics-based multiscale internal-variable models of plasticity, including a variety of size-dependent effects and interface mechanisms [9,18– 26]. In
this context it should be emphasized that the FE method itself is not the actual model but the variational
solver for the underlying constitutive equations that map the anisotropy of elastic–plastic shears associated with the various types of lattice defects (e.g. dislocations, twins, martensite). Since
its first introduction by Peirce et al. in 1982 [27] the CPFE method has matured into a whole family
of constitutive and numerical formulations that has been applied to a broad variety of crystal mechanical problems
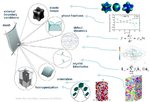
More specific this article reviews continuum-based variational formulations for describing the elastic–plastic deformation of anisotropic heterogeneous crystalline matter. These approaches, commonly
referred to as crystal plasticity finite-element models, are important both for basic microstructure-based mechanical predictions as well as for engineering design and performance simulations
involving anisotropic media. Besides the discussion of the constitutive laws, kinematics, homogenization schemes and multiscale approaches behind these methods, we also present some examples,
including, in particular, comparisons of the predictions with experiments. The applications stem from such diverse fields as orientation stability, microbeam bending, single-crystal and bicrystal
deformation, nanoindentation, recrystallization, multiphase steel (TRIP) deformation, and damage prediction for the microscopic and mesoscopic scales and multiscale predictions of rolling textures,
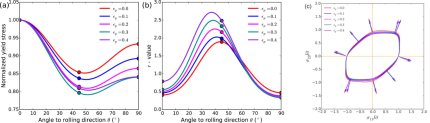
cup drawing, Lankfort (r) values and stamping simulations for the macroscopic scale.
The crystal plasticity finite element constitutive methods have increasingly gained momentum in the field of materials modeling and particularly multicsale mechanical and micromechanical modeling. In these approaches one typically assumes the stress response at each macroscopic continuum material point to be potentially given by one crystal or by a volume-averaged response of a set of grains comprising the respective material point. The latter method naturally involves local homogenization. Compared to isotropic J2 approaches the crystal plasticity finite element method reduces the degrees of freedom for the displacement field at each integration point to the crystallographic slip dyades transformed according to the local grain orientation. Representing and updating the crystallographic orientation at each Gauss point renders crystallographically discrete plasticity simulations powerful tools for investigating anisotropy and the evolution of deformation textures.
Using texture components in crystal plasticity
finite element simulations
raabe_roters_texture_components_IJP_2003[...]
PDF-Dokument [841.7 KB]
International Journal of Plasticity 20 (2004) 339
Here we present methods to map crystallographic textures in crystal plasticity finite element simulations. Fourier-type series expansion methods which use spherical harmonic
library functions as well as the direct pole figure inversion methods are not well suited to reproduce texture information in a sufficiently localized spherical form onto finite element
grids. Mathematically compact Gauss-shaped spherical texture components represent a better approach
for including textures in finite element models since they represent an excellent compromise between discreteness (spherical localization), compactness (simple functions),
mathematical precision (very good approximation also of complex orientation distribution functions already with small sets of texture components), scalability (the number of used texture
components can be systematically varied according to the desired exactness of the texture fit),
conceptual simplicity (simple mathematical handling), and physical significance (texture components can be directly linked to characteristic metallurgical mechanisms). The use of texture
component functions has also advantages over the use of large sets of discrete single orientations with equal scatter and height since they are more compact, practical, and provide better
physical insight into microstructural mechanisms and composition sensitive effects. The
article presents a new approach for the mathematical reproduction of such crystallographic texture components in crystal plasticity finite element simulations. It explains in some
detail why they are particularly suited for this purpose and how they can be used to map and recover textures in/from plasticity simulations.
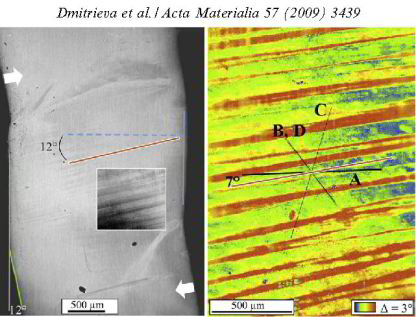
Lamination microstructure in shear deformed copper single crystals
Olga Dmitrieva, Patrick W. Dondl, Stefan Müller, Dierk Raabe
Acta Materialia 57 (2009) 3439-3449
Acta Materialia 57 (2009) 3439 Laminatio[...]
PDF-Dokument [863.1 KB]
We investigate the formation of microscopic patterns in a copper single crystal deformed in a shear experiment. Using high-resolution electron backscatter diffraction imaging, we find a band-like microstructure consisting of confined areas in the sample with rotated lattice. Digital image correlation allows us to exactly determine the macroscopic state of deformation of the sample. This data can be used as a side condition to calculate the lamination parameters from the theory of kinematically compatible lamination of separate material regions, each deforming in single slip. The parameters given by the theory agree with the measured properties, i.e. a lattice rotation of 3 and a lamination normal rotated 7° counterclockwise from a <111> direction.
International Journal of Plasticity 23 (2007) 690
Chung-Souk Han, Anxin Ma, Franz Roters, Dierk Raabe
A Finite Element approach with patch projection for strain gradient plasticity formulations
International Journal of Plasticity 23 ([...]
PDF-Dokument [787.4 KB]
Several strain gradient plasticity formulations have been suggested in the literature to account for inherent size effects on length scales of microns and submicrons. The necessity of strain gradient related terms render the simulation with strain gradient plasticity formulation computationally very expensive because quadratic shape functions or mixed approaches in displacements and strains are usually applied. Approaches using linear shape functions have also been suggested which are, however, limited to regular meshes with equidistanced Finite Element nodes. As a result the majority of the simulations in the literature deal with plane problems at small strains. For the solution of general three dimensional problems at large strains an approach has to be found which has to be computationally affordable and robust. For this goal a strain gradient Finite Element approach is suggested where elements with linear shape functions are applied in combination with a patch projection technique well known from error indication and adaptive mesh procedures. This approach is applied to a strain gradient crystal plasticity formulation where strain gradients are incorporated in terms of geometrically necessary dislocation densities. Simulation results of size dependent problems, including laminates in simple shear and a three dimensional contact problem, are presented and discussed to assess the performance of the suggested approach
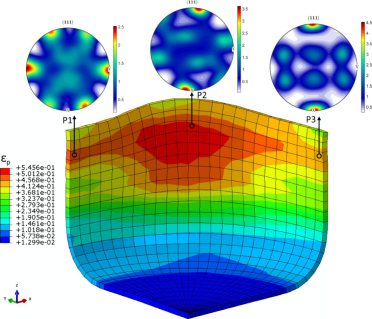
In the modern practice of stamping simulation of complex industrial parts the prediction of springback still lacks accuracy. In commercial software packages various empirical constitutive laws for sta
Computational Materials Science 46 (2009[...]
PDF-Dokument [2.5 MB]
In the modern practice of stamping simulation of complex industrial parts the prediction of springback still lacks accuracy. In commercial software packages various empirical constitutive laws for stamping are available. Limited to simple empirical models for material anisotropy they do not take into account in a full manner the effects of microstructure and its evolution during the deformation process. The crystal plasticity finite element method bridges the gap between the polycrystalline texture and macroscopic mechanical properties that opens the way for more profound consideration of metal anisotropy in the stamping process simulation. In this paper the application of crystal plasticity FEM within the concept of virtual material testing with a representative volume element (RVE) is demonstrated. Using virtual tests it becomes possible, for example, to determine the actual shape of the yield locus and Lankford parameters and to use this information to calibrate empirical constitutive models. Along with standard uniaxial tensile tests other strain paths can be investigated like biaxial tensile, compressive or shear tests. The application of the crystal plasticity FEM for the virtual testing is demonstrated for DC04 and H320LA steel grades. The parameters of the Vegter yield locus are calibrated and the use case demonstration is completed by simulation of a typical industrial part in PAMSTAMP 2G.
Intern J Plasticity 25 (2009) 1655 damag[...]
PDF-Dokument [2.8 MB]
International Journal of Plasticity 25 (2009) 1655
The mechanical response of engineering materials evaluated through continuum fracture mechanics typically assumes that a crack or void initially exists, but it does not provide
information about the nucleation of such flaws in an otherwise flawless microstructure. How such flaws originate, particularly at grain (or phase) boundaries is less clear.
Experimentally, ‘‘good” vs. ‘‘bad” grain boundaries are often invoked as the reasons for critical damage
nucleation, but without any quantification. The state of knowledge about deformation at or near grain boundaries, including slip transfer and heterogeneous deformation, is reviewed to show
that little work has been done to examine how slip interactions can lead to damage nucleation. A fracture initiation parameter developed recently for a low ductility model material
with limited slip systems provides a new definition of grain boundary character based upon operating slip and twin systems (rather than an interfacial energy based definition). This
provides a way to predict damage nucleation density on a physical and local (rather than a statistical) basis. The parameter assesses the way that highly activated twin systems are
aligned with principal stresses and slip system Burgers vectors. A crystal plasticity-finite element method (CP-FEM) based model of an extensively characterized microstructural region
has
been used to determine if the stress–strain history provides any additional insights about the relationship between shear and damage nucleation. This analysis shows that a combination of a
CP-FEM model augmented with the fracture initiation parameter shows promise for becoming a predictive tool for identifying damageprone boundaries.
The solution of a continuum mechanical boundary value problem requires a constitutive response that connects deformation and stress at each material point. Such connection can be regarded as three sep
MPIE-DAMASK-Introduction.pdf
PDF-Dokument [1.4 MB]
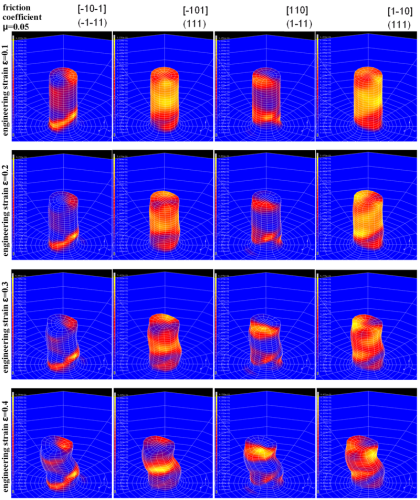
Effects of initial orientation, sample geometry and friction on anisotropy and crystallographic orientation changes in single crystal microcompression deformation: A crystal plasticity finite element
Acta Materialia 55 (2007) 4567 CPFEM Pil[...]
PDF-Dokument [2.2 MB]
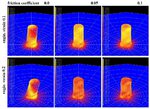
The study presents crystal plasticity finite element simulations of cylindrical Cu single crystal micropillar compression tests. The aim is to study the influence of the stability of the
initial crystal orientation, sample geometry (diameter-to-length ratio) and friction on the anisotropy and crystallographic orientation changes during such tests. Initial anisotropy (initial
orientation) has a strong influence on
the evolution of crystallographic orientation changes and also, to a minor extent, on the sample shape during compression. Pronounced orientation changes occur at an early stage of compression
(at engineering strains of 0.2), entailing as a rule a large orientation spread within the initially uniformly oriented sample. A non-zero friction has a stabilizing effect on the course of the
compression test even in cases where strong orientation changes occur. The evolution of orientation changes during compression is in part due to rigid body rotations
(shape inclination due to buckling) rather than exclusively to crystallographic reorientation. Orientations that are crystallographically unstable and non-symmetric during compression tend to
entail shape instability of the pillars at an earlier stage than observed for more stable cases.
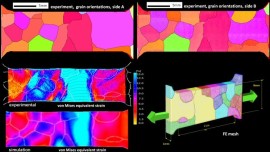
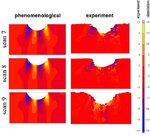
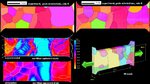
The mechanical response of multiphase alloys is governed by the microscopic strain and stress partitioning behavior among microstructural constituents. However, due to limitations in the characterization of the partitioning that takes place at the submicron scale, microstructure optimization of such alloys is typically based on evaluating the averaged response, referring to, for example, macroscopic stress–strain curves. Here, a novel experimental–numerical methodology is introduced to strengthen the integrated understanding of the microstructure and mechanical properties of these alloys, enabling joint analyses of deformation-induced evolution of the microstructure, and the strain and stress distribution therein, down to submicron resolution. From the experiments, deformation-induced
Tasan et al Acta Materialia vol 91 2014 [...]
PDF-Dokument [3.4 MB]
The mechanical response of multiphase alloys is governed by the microscopic strain and stress partitioning behavior among microstructural constituents. However, due to limitations in the
characterization of the partitioning that takes place at the submicron scale, microstructure optimization of such alloys is typically based on evaluating the averaged response, referring to, for
example, macroscopic stress–strain curves. Here, a novel experimental–numerical methodology is introduced to strengthen the integrated understanding of the
microstructure and mechanical properties of these alloys, enabling joint analyses of deformation-induced evolution of the microstructure, and the strain and stress distribution therein, down to
submicron resolution. From the experiments, deformation-induced evolution of (i) the microstructure, and (ii) the local strain distribution are concurrently captured, employing in situ secondary
electron imaging and electron backscatter diffraction (EBSD) (for the former), and microscopic-digital image correlation (for the latter). From the simulations,
local strain as well as stress distributions are revealed, through 2-D full-field crystal plasticity (CP) simulations conducted with an advanced spectral solver suitable for heterogeneous
materials. The simulated model is designed directly from the initial EBSD measurements, and the phase properties are obtained by additional inverse CP simulations of nanoindentation experiments
carried out on the original microstructure. The experiments and simulations demonstrate good correlation in the proof-of-principle study conducted here on a martensite–ferrite dual-phase
steel, and deviations are discussed in terms of limitations of the techniques involved. Overall, the presented integrated computational materials engineering approach provides a vast amount of
well-correlated structural and mechanical data that enhance our understanding as well as the design capabilities of multiphase alloys.
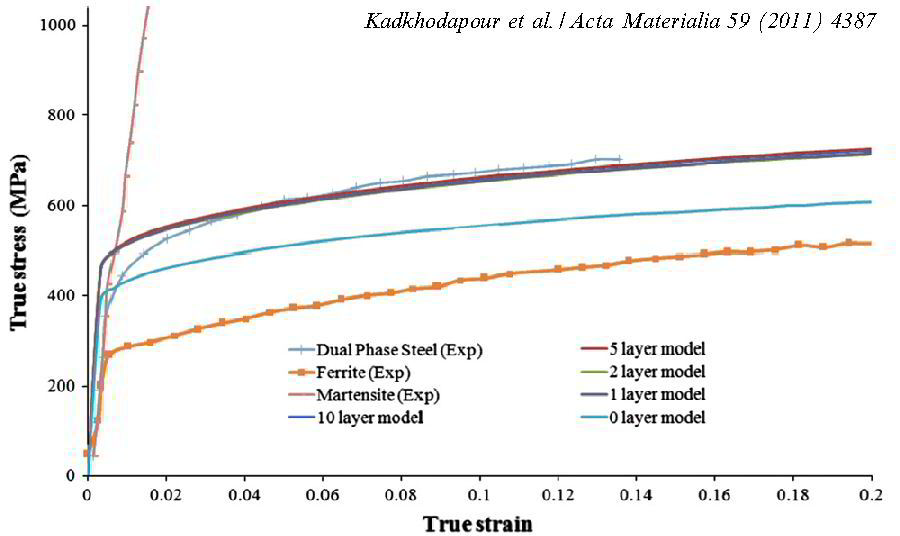
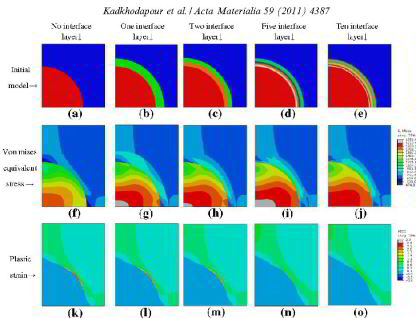
J. Kadkhodapour, S. Schmauder, D. Raabe, S. Ziaei-Rad, U. Weber, M. Calcagnotto
Acta Materialia 59 (2011) 4387-4394
Experimental and numerical study on geometrically necessary dislocations and non-homogeneous mechanical properties of the ferrite phase in dual phase steels
Acta Materialia 59 (2011) 4387-4394 dual[...]
PDF-Dokument [620.1 KB]
The microstructure of dual phase steels can be compared with a composite composed of a matrix of ferrite reinforced by small islands of martensite. This assumption has been used in several
attempts to model the mechanical properties of dual phase steels. However, recent measurements show that the properties of the ferrite phase change with distance from the martensite grains.
These measurements showed that the grains of the ferrite phase are harder in the vicinity of martensite grains. As a consequence of this local hardening effect,
the ferrite phase has to be considered as an inhomogeneous matrix in modeling dual phase steels. This experiment inspired the idea that local hardening is caused by geometrically necessary
dislocations. The idea is investigated experimentally and numerically in the present analysis, which for the first time leads to good agreement with experimental observations of the mechanical
stress–strain behavior.
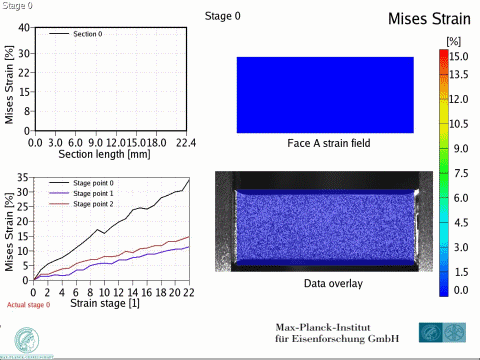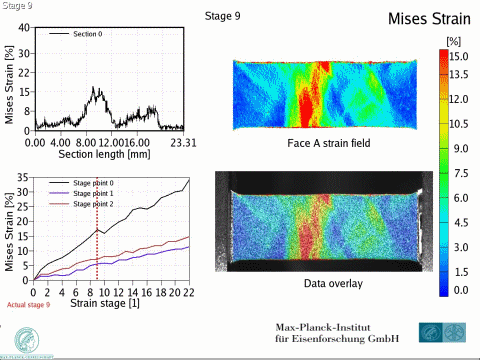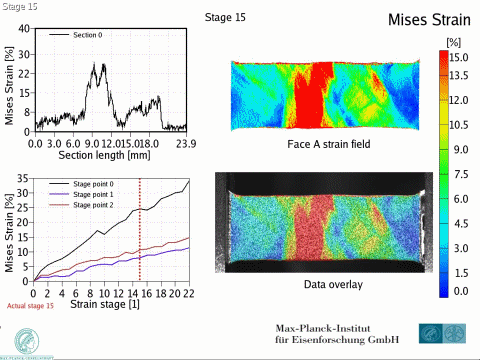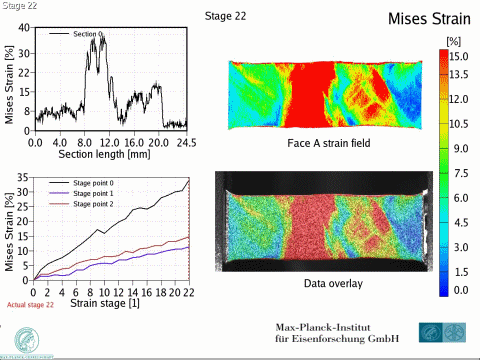
Dual phase steels deform in a heterogeneous manner, i.e. with strain and stress partitioning. Such heterogeneity leads to a spatially heterogeneous damage distribution, and thus, plays an important role in damage inheritance and fracture. To better understand DP steels, we here identify connections between the strain and damage heterogeneity and the microstructural parameters, e.g. ferrite grain size, martensite distribution and martensite fraction. We conduct in-situ deformation experiments on two different DP steel grades, employing two different microscopic-digital image correlation (lDIC) techniques to achieve strain maps. The strain maps are analyzed in connection to the observed damage incidents (identified by image post-processing) and to local stress maps.
Intern Journ Plasticity 63 (2014) 198 In[...]
PDF-Dokument [964.9 KB]
J Mechanics Physics Solids vol 58 (2010)[...]
PDF-Dokument [956.1 KB]
Acta Materialia 50 (2002) 421-440
Theory of orientation gradients in plastically strained crystals
D. Raabe, Z. Zhao, S.-J. Park, F. Roters
Acta Materialia 50 (2002) 421 theory ori[...]
PDF-Dokument [728.5 KB]
We suggest a theory of in-grain orientation gradients in plastically strained metals. It is an approach to explain why initially uniformly oriented crystals can—under gradient-free external
loadings—build up in-grain orientation gradients
during plastic deformation and how this phenomenon depends on intrinsic factors (crystal orientation) and extrinsic factors (neighbor grains). The intrinsic origin (orientation dependence)
of in-grain orientation gradients is investigated by quantifying the change in crystal reorientation upon small changes in initial orientation. This part of the approach is formulated
by applying a divergence operator to reorientation rate vector fields (in the present paper calculated by using strain-rate homogenization Taylor–Bishop–Hill theory). The obtained scalar
divergence function (but not the reorientation vector field itself) quantifies the kinematic stability of grains under homogeneous boundary conditions as a function of their orientation.
Positive divergence (source in the reorientation rate vector field) characterizes orientations with diverging non-zero reorientation rates which are kinematically unstable and prone to build up
orientation gradients. Zero divergence indicates orientations with reorientation rate identity with the surrounding orientations which are not prone to build up orientation gradients.
Negative divergence (sink in the reorientation rate vector field) characterizes orientations with converging non-zero reorientation rates which are kinematically stable and not prone to build up
orientation gradients. Corresponding results obtained by use of a crystal plasticity finite element formulation are in good agreement with the reorientation field divergence function
derived by homogenization theory. The extrinsic origin of in-grain orientation gradients (influence of grain–neighbor interaction) is addressed using a crystal plasticity finite element
bicrystal model. The simulations show that a significant dependence of orientation gradients on the neighbor crystals occurs for grains with high positive divergence. The build-up of orientation
gradients in grains with close to zero or negative divergence is in body centered cubic crystals less sensitive to the presence of neighbor orientations than in face centered cubic crystals
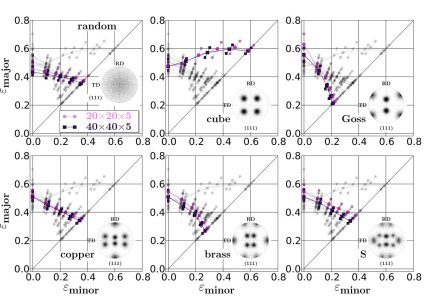
(Goss and cube orientation).
Acta Materialia 60 (2012) 1623-1632
Polycrystal model of the mechanical behavior of a Mo–TiC30 vol.%
metal–ceramic composite using a three-dimensional microstructure map obtained by dual beam focused ion beam scanning electron microscopy
D. Cedat, O. Fandeur, C. Rey, D. Raabe
Acta Materialia 60 (2012) 1623 3D crysta[...]
PDF-Dokument [638.3 KB]
The mechanical behavior of a Mo–TiC30 vol.% ceramic–metal composite was investigated over a wide temperature range (25–700 °C). High-energy X-ray tomography was used to reveal percolation of
the hard titanium carbide phase through the composite. Using a polycrystal approach for a two-phase material, finite-element simulations were performed on a real three-dimensional (3-D) aggregate of
the material. The 3-D microstructure, used as the starting configuration for the predictions, was obtained by serial sectioning in a dual beam focused ion beam scanning electron microscope
coupled to an electron backscattered diffraction system. The 3-D aggregate consists of a
molybdenum matrix and a percolating TiC skeleton. As for most body-centered cubic (bcc) metals, the molybdenum matrix phase is characterized by a change in plasticity mechanism with temperature.
We used a polycrystal model for bcc materials which was extended to two phases (TiC and Mo). The model parameters of the matrix were determined from experiments on pure molydenum. For all
temperatures investigated the TiC particles were considered to be brittle. Gradual damage to the TiC particles was treated, based on an accu-
mulative failure law that is approximated by evolution of the apparent particle elastic stiffness. The model enabled us to determine the evolution of the local mechanical fields with deformation
and temperature. We showed that a 3-D aggregate representing the actual microstructure of the composite is required to understand the local and global mechanical properties of the composite
studied.