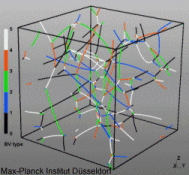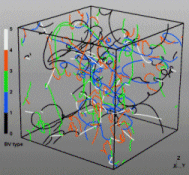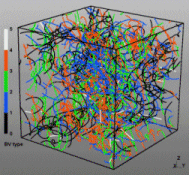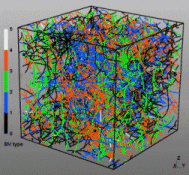
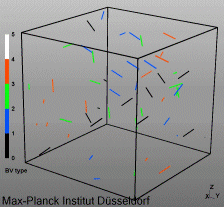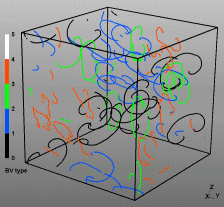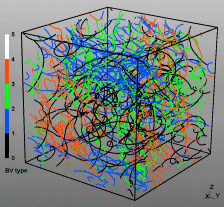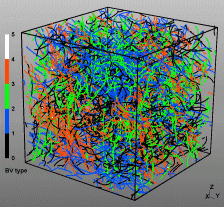
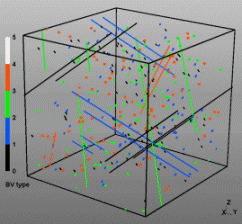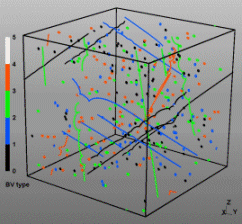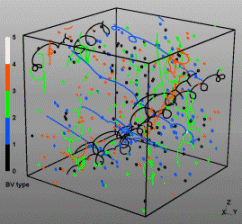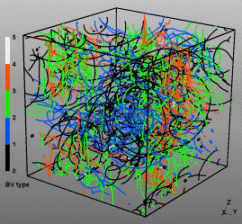
Discrete Dislocation Dynamics Simulations (DDD)

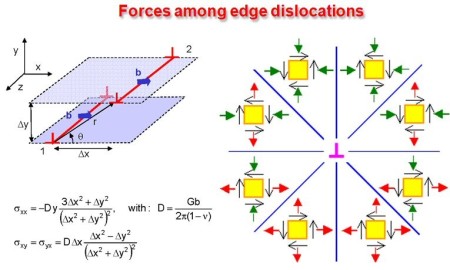
The dislocation dynamics simulations discussed on this webpage were conducted using a modified version of the ParaDiS code (DD code developed at Lawrence Livermore National Laboratory). The approach simulates a dislocation network represented by a set of nodes connected by line segments. One stable dislocation node connects a maximum of four segments (arms). Each segment carries a Burgers vector and is assigned a glide plane normal. The conservation of the Burgers vector is assured everywhere in the dislocation network, except at a pinned node with a single arm (e.g. the end points of a Frank–Read source). The force on a dislocation node due to the stress field of its own arms and other segments in the system is calculated based on the non-singular, self-consistent stress field and elastic energy expressions. The nodal force exerted by external loading is calculated through the Peach–Köhler equation. The nodal velocity is proportional to the projected nodal force by a mobility tensor. The topology update of a dislocation network in the ParaDiS code reflects the physics of dislocation motion and collisions in real crystals: Burgers vector reactions (annihilation, junction zipping and unzipping) happen naturally through the collisions and dissociations of dislocation nodes.