Mechanics of semi-crystalline polymers

Semi-crystalline polymers are increasingly used in structural applications where the influence of the microstructure and its evolution on the macroscopic mechanical properties is of prime importance. A number of applications, such as thin films, coatings, high-modulus fibers and ribbons, display highly anisotropic mechanical and crystallographic properties and their processing often involves large plastic deformation of an initially isotropic material.

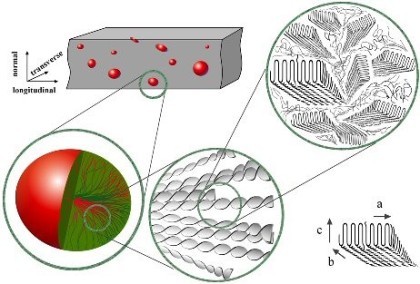
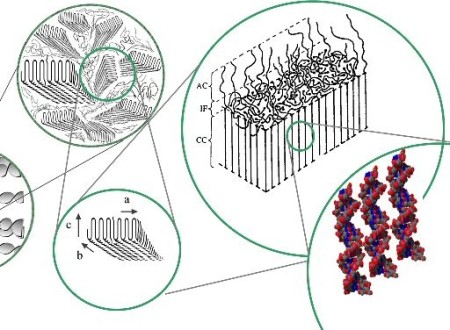
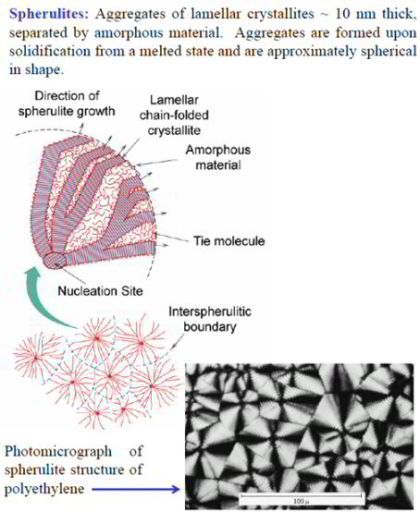
The microstructure of melt-crystallized polymers consists of broad, thin crystalline lamellae separated by amorphous layers. Locally, the lamellae are grown from a central nucleus and are radially oriented, which results in the formation of spherulitic structures. During large plastic deformation, profound changes in both the crystallographic texture and morphology take place. It has been observed that in uniaxial tension of HDPE, the initial lamellar microstructure is gradually destroyed and replaced by stretched fibrils. Similar lamellar-to-fibrillar transition processes have also been reported from simple-shear experiments of HDPE.

In this work a self-consistent model for describing the mechanics of semi-crystalline polymers is proposed to study their constitutive behavior, crystallographic texture and morphology evolution during large plastic deformation. The material is considered as an aggregate of composite inclusions, each representing a stack of crystalline lamellae with their adjacent amorphous layers. The deformation within the inclusions is volume-averaged
over the phases. The interlamellar shear is modeled as an additional slip system with a slip direction depending on the inclusion’s stress. Hardening of the amorphous phase due to molecular orientation and, eventually, coarse slip, is introduced via Arruda–Boyce hardening law for the corresponding plastic resistance. The morphology evolution is accounted for through the change of shape of the inclusions under the applied deformation gradient. The overall behavior is obtained via a viscoplastic tangent self-consistent scheme. 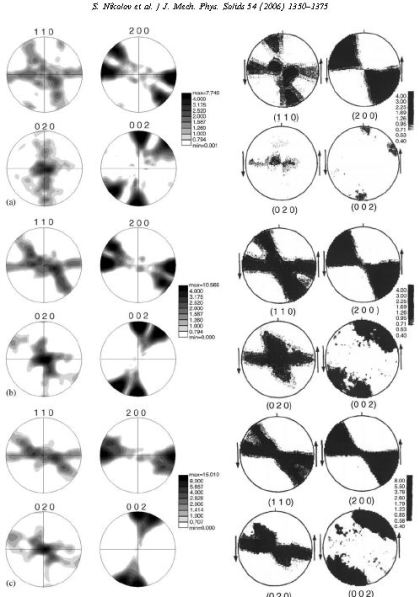The model is applied to high density polyethylene (HDPE). The stress–strain response, texture and morphology changes are simulated under different modes of straining and compared to experimental data as well as to the predictions of other models.

In the past fifteen years, several micromechanical models have been developed in order to simulate the stress–strain behavior and crystallographic texture evolution in semicrystalline polymers at large strains. Parks and Ahzi (1990) proposed a purely crystalline model treating the lack of five independent slip systems in polymer crystals. Ahzi et al. (1990) developed a bi-crystal approach, where the basic structural unit of semi-crystalline polymers was introduced as a two-phase composite inclusion consisting of a single, flat lamella and its adjacent amorphous layer (Fig. 2a). Both models used Taylor’s assumption for the overall properties. This approach yields a very stiff stress–strain response and overestimates the rate of the texture evolution. Dahoun et al. (1991) represented the crystalline polymer as an aggregate of crystalline lamellae in the form of oblate ellipsoids.
The average properties have been found via a tangent self-consistent scheme. Due to the more realistic modeling of the interactions between the crystals, the obtained results agreed reasonably well with the experiments despite the fact that the amorphous phase contribution was not considered. Later, Lee et al. (1993a) used the composite inclusion depicted in Fig. 2a, coupled with Sachs- and self-consistent-like interaction laws. The model produced valuable results about the stress–strain behavior and crystallographic texture development of HDPE. Recently, van Dommelen et al. (2003) extended the rigid-viscoplastic modeling of Lee et al. (1993a) to elasto–viscoplastic behavior using a deformation gradient formulation and the same composite inclusion model. With this approach they were able to simulate cyclic loadings of semi-crystalline polymers.
Despite the above mentioned efforts, many important phenomena related to the strain-induced evolution of the microstructure are not fully accounted for in the existing models.
For example, there were no attempts to incorporate the strain localization within the crystals and their subsequent fragmentation into smaller blocks, the strain-induced decrease in crystallinity (Raabe et al., 2004) or the transformation of the morphology from a lamellar to a fibrillar state (Fig. 1). Undoubtedly, all of these microscopic processes influence the macroscopic mechanical properties and their integration into the constitutive modeling should result in better predictions of the observed stress–strain response and texture evolution. In the present work, we develop a micromechanical model which, besides the stress–strain behavior and the crystallographic texture evolution, also takes into account the morphology evolution of the microstructure. We restrict our attention to monotonic loadings. The material is assumed to be incompressible. For the sake of simplicity, elasticity is neglected, which is a reasonable approximation for highly crystalline polymers and polymers with glassy amorphous phase where the purely elastic strain does not exceed 3%. Following Lee et al. (1993a), we ignore the radial arrangement of the lamellae in the spherulites and use a basic structural unit representing only a part of a spherulite. This simplification is motivated by the fact that, despite some efforts in this direction, the influence of the spherulitic structure as such on the macroscopic mechanical properties has not been proven experimentally. Moreover, at large deformations the spherulites are gradually destroyed (Bartczak et al., 1992a). With these considerations in mind, here we assume that an aggregate consisting of randomly oriented composite inclusions, which are smaller than the spherulites, behaves in the same way as an aggregate where the inclusions are arranged in spherulitic-like structures as long as the macroscopic mechanical properties are concerned. In contrast to the inclusion model used by Lee et al. (1993a), we define the basic structural unit of semi-crystalline polymers as a stack of crystalline lamellae with their adjacent amorphous layers according to Fig. 2b (Nikolov and Doghri, 2000).