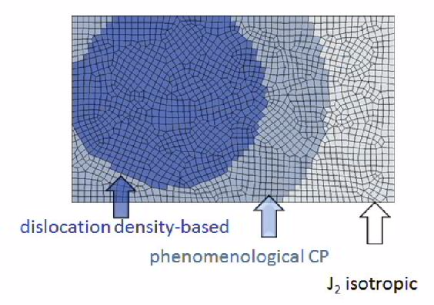
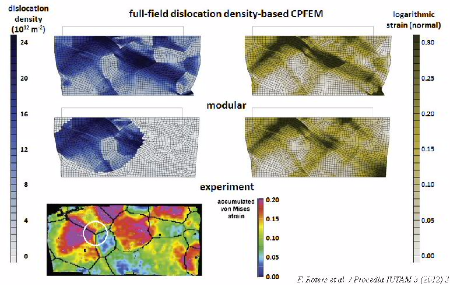
Dislocation-based Crystal Plasticity Finite Element Method
Why using dislocation - density based constitutive laws in crystal plasticity modeling?
In contrast to phenomenological constitutive models used in conventional viscoplastic crystal plasticity simulations, physics-based constitutive laws aim at relying on internal variables.
In constitutive modeling in materials science we refer to such variables as internal variables which have microstructural meaning such as lattice defect densities.
In the case of plasticity the most important microstructural state variable certainly is the dislocation density as dislocations are the elementary carriers of plastic deformation.
Models that treat the evolution of dislocation densities and calculate the flow stress from them have been proposed by various authors as outlined in the following:
During the past two decades multiple efforts were made to explicitly incorporate dislocation density-based constitutive laws into crystal plasticity finite element and spectral (Fast Fourier) models e.g. Alankar et al. (2012a, 2009), Aoyagi et al. (2013), Arsenlis and Parks (2002), Arsenlis and Tang (2003), Cheong and Busso (2004), Evers et al. (2004), Erieau and Rey (2004), Lim et al. (2011), Ma et al. (2006), Mayeur et al. (2011), Ortiz et al. (2000) and Shanthraj and Zikry (2011).
A detailed review of dislocation density based crystal plasticity models has been provided by Roters et al. (2010). While most of these modeling approaches are phenomenological, i.e. some of these use the dislocation density as power law dependent variable (e.g. Lim et al. (2011)), other approaches include them as self sustained geometric loops (e.g. Arsenlis and Parks (2002)).
The dislocation density based approach in the context of crystal plasticity finite element modeling is employed not only for understanding single crystal behavior but also for simulations of polycrystal plasticity, e.g. by Austin and McDowell (2011), Erieau and Rey (2004) and Lim et al. (2011). However, when studying macroscopic plastic anisotropy in metal forming processes, most finite element (FE) approaches use viscoplastic crystal plasticity or even Taylor-based homogenization approximations rather than internal variable dislocation based constitutive laws.
Some of the approaches currently in use or under further development are presented below:
Acta Materialia 54 (2006) 2169-2179
Acta Materialia 54 (2006) 2169 GND in CP[...]
PDF-Dokument [535.3 KB]
A dislocation density based constitutive model for face-centred cubic crystals is introduced and implemented into a crystal plasticity finite element framework. The approach assumes a
homogeneous dislocation structure and tracks the dislocation evolution on each slip system. In addition to the statistically stored dislocations, the geometrically necessary dislocation density
is introduced in order to consider strain gradients and thus render the model size sensitive. Furthermore, we develop a consistent algorithm for the updating of the
geometrically necessary dislocation density. A simple shear experiment of an aluminium single crystal is used to calibrate the material parameters of the model and demonstrate its size
sensitivity.
Acta Materialia 58 (2010) 1152-1211
Crystal Plasticity Finite Element Modeli[...]
PDF-Dokument [3.6 MB]
This article reviews continuum-based variational formulations for describing the elastic–plastic deformation of anisotropic heterogeneous crystalline matter. These approaches, commonly referred to as crystal plasticity finite-element models, are important both for basic microstructure-based mechanical predictions as well as for engineering design and performance simulations involving anisotropic media. Besides the discussion of the constitutive laws, kinematics, homogenization schemes and multiscale approaches behind these methods, we also present some examples, including, in particular, comparisons of the predictions with experiments. The applications stem from such diverse fields as orientation stability, microbeam bending, single-crystal and bicrystal deformation, nanoindentation, recrystallization, multiphase steel (TRIP) deformation, and damage prediction for the microscopic and mesoscopic scales and multiscale predictions of rolling textures, cup drawing, Lankfort (r) values and stamping simulations for the macroscopic scale.
Dislocation based constitutive model for crystal plasticity simulations
In this work we suggest a dislocation based constitutive model to incorporate the mechanical interaction between mobile dislocations and grain boundaries into a crystal plasticity finite
element framework. The approach is based on the introduction of an additional activation energy into the rate equation for mobile dislocations in the vicinity of grain boundaries. The energy
barrier is derived by using a geometrical model for thermally activated dislocation penetration events through grain boundaries. The model takes full account of the geometry of the grain
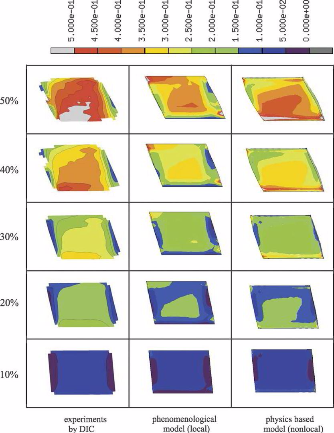
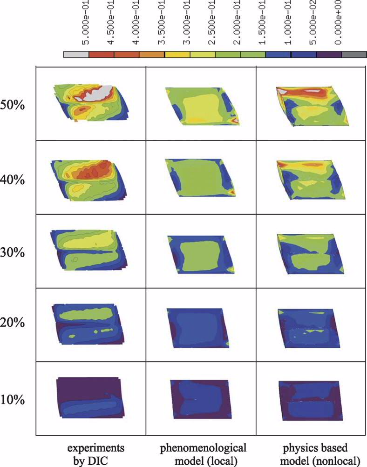
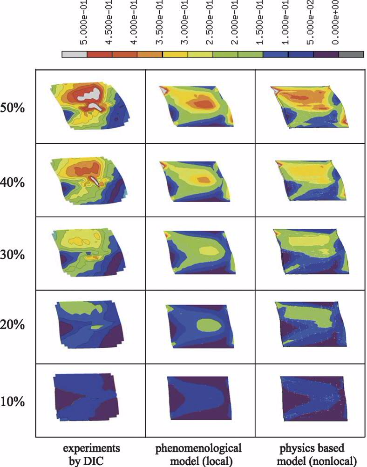
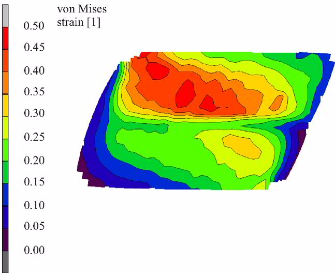
boundaries and of the Schmid factors of the critically stressed incoming and outgoing slip systems and is formulated as a vectorial conservation law. The new model is applied to the case of 50%
(frictionless) simple shear deformation of Al bicrystals with either a small, medium, or large angle grain boundary parallel to the shear plane. The simulations are in excellent agreement
with the experiments in terms of the von Mises equivalent strain distributions and textures. The study reveals that the incorporation of the misorientation alone is not sufficient to
describe the influence of grain boundaries on polycrystal micro-mechanics. We observe three mechanisms which jointly entail pronounced local hardening in front of grain boundaries (and other
interfaces) beyond the classical kinematic hardening effect which is automatically included in all crystal plasticity finite element models owing to the change in the Schmid factor across
grain boundaries. These are the accumulation of geometrically necessary dislocations (dynamic effect; see [Ma A, Roters F, Raabe D. A dislocation density based constitutive model for crystal
plasticity FEM including geometrically necessary dislocations. Acta Mater 2006;58:2169–79]), the resistance against slip penetration (dynamic effect; this paper), and the change in the
orientation spread
(kinematic effect; this paper) in the vicinity of grain boundaries.
Acta Materialia 54 (2006) 2181-2194
Acta Materialia 54 (2006) 2181 CPFEM bic[...]
PDF-Dokument [2.3 MB]
International Journal of Plasticity 52 (2014) 18-32
Intern Journ Plasticity 52 (2014) page 1[...]
PDF-Dokument [2.3 MB]
Here we present a single crystal plasticity model based on edge and screw dislocation densities for body centered cubic (bcc) crystals. In a bcc crystal screw dislocations experience
high lattice friction due to their non-planar core. Hence, they have much slower velocity compared to edge dislocations. This phenomenon is modeled by accounting for the motion of screw
dislocations via nucleation and expansion of kink-pairs. The model, embedded as a constitutive law into a crystal plasticity framework, is able to predict the crystallographic
texture of a bcc polycrystal subjected to 70%, 80% and 90% thickness reduction. We perform a parametric study based on the velocities of edge and screw dislocations to analyze the effect on
plastic anisotropy of electro-deposited pure iron with long needle-shaped grains having sharp crystallographic <111>//ND texture (ND: normal direction). The model shows a large change
in the r-value (Lankford value, planar anisotropy ratio) for pure iron when the texture changes from random to <111>//ND. For different simulated cases where the crystallites have an
orientation deviation of 1°, 3° and 5°, respectively, from the ideal
<111>//ND axis, the simulations predict r-values between 4.0 and 7.0 which is in excellent agreement with data observed in experiments by Yoshinaga et al. (ISIJ Intern., 48
(2008) 667–670). For these specific orientations of grains, we also model the effect of long needle shaped grains via a procedure that excludes dislocation annihilation.
Acta Materialia 59 (2011) 7003-7009
Acta Materialia 59 (2011) 7003 titanium [...]
PDF-Dokument [337.4 KB]
A new constitutive plasticity model for prismatic slip in hexagonal a-titanium is developed. In the concept pure edge and screw dislocation densities evolve on the {1010} <1210> slip systems. The model considers that the screw dislocation segments have a spread out core, leading to a much higher velocity of edge compared with screw dislocations. This enables the model to describe the observed transition in strain hardening from stage I to stage II in single crystals oriented for prismatic slip. Good agreement is found between the experimentally observed and simulated stress–strain behavior.
International Journal of Solids and Structures 43 (2006) 7287-7303
IntJ Solids Struct 43 (2006) 7287 CPFEM [...]
PDF-Dokument [761.2 KB]
A dislocation density based constitutive model for the face centered cubic crystal structure has been implemented into a crystal-plasticity finite element framework and extended to consider the mechanical interaction between mobile dislocations and grain boundaries by the authors [Ma, A., Roters, F., Raabe, D., 2006a. A dislocation density based constitutive model for crystal-plasticity FEM including geometrically necessary dislocations. Acta Materialia 54, 2169–2179; Ma, A., Roters, F., Raabe, D., 2006b. On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling – theory, experiments, and simulations. Acta Materialia 54, 2181–2194]. The approach to model the grain boundary resistance against slip is based on the introduction of an additional activation energy into the rate equation for mobile dislocations in the vicinity of internal interfaces. This energy barrier is derived from the assumption of thermally activated dislocation penetration events through grain boundaries. The model takes full account of the geometry of the grain boundaries and of the Schmid factors of the critically stressed incoming and outgoing slip systems. In this study we focus on the influence of the one remaining model parameter which can be used to scale the obstacle strength of the grain boundary.
Procedia IUTAM 3 ( 2012 ) 3 – 10
Procedia IUTAM 3 ( 2012 ) 3 MPIE DAMASK [...]
PDF-Dokument [1.4 MB]
The solution of a continuum mechanical boundary value problem requires a constitutive response that connects deformation and stress at each material point. Such connection can be regarded as
three separate hierarchical problems.
At the top-most level, partitioning of the (mean) boundary values of the material point among its microstructural constituents and the associated homogenization of their response is required,
provided there is more than one constituent
present. Second, based on an elastoplastic decomposition of (finite strain) deformation, these responses follow from explicit or implicit time integration of the plastic deformation rate per
constituent. Third, to establish the latter, a state
variable-based constitutive law needs to be interrogated and its state updated.
The Düsseldorf Advanced MAterial Simulation Kit (DAMASK) reflects this hierarchy as it is built in a strictly modular way. This modular structure makes it easy to add additional constitutive
models as well as homogenization
schemes. Moreover it interfaces with a number of FE solvers as well as a spectral solver using an FFT. We demonstrate the versatility of such a modular framework by considering three scenarios:
Selective refinement of the constitutive material description within a single geometry, component-scale forming simulations comparing different homogenization schemes, and comparison of
representative volume element simulations based on the FEM and the spectral solver.
GAMM-Mitt. 38, No. 2, 213 – 227 (2015) / DOI 10.1002/gamm.201510012
Cereceda et al 2015 GAMM Mitteilungen vo[...]
PDF-Dokument [445.2 KB]
Understanding and improving the mechanical properties of tungsten is a critical task for the materials fusion energy program. The plastic behavior in body-centered cubic (bcc)
metals like tungsten is governed primarily by screw dislocations on the atomic scale and by ensembles and interactions of dislocations at larger scales. Modeling this behavior requires
the application of methods capable of resolving each relevant scale. At the small scale, atomistic
methods are used to study single dislocation properties, while at the coarse-scale, continuum models are used to cover the interactions between dislocations. In this work we present
a multiscale model that comprises atomistic, kinetic Monte Carlo (kMC) and continuum-level crystal plasticity (CP) calculations. The function relating dislocation velocity to applied
stress
and temperature is obtained from the kMC model and it is used as the main source of constitutive information into a dislocation-based CP framework. The complete model is used to perform
material point simulations of single-crystal tungsten strength. We explore the entire crystallographic orientation space of the standard triangle. Non-Schmid effects are inlcuded
in the model by considering the twinning-antitwinning (T/AT) asymmetry in the kMC calculations. We consider the importance of 1 1 1{1 1 0} and 1 1 1{1 1 2} slip systems in the homologous
temperature range from 0.08Tm to 0.33Tm, where Tm=3680 K is the melting point in tungsten.
Acta Materialia 71 (2014) 333-348
Acta Materialia 71 (2014) 333 crystal pl[...]
PDF-Dokument [1.4 MB]
We present a physics-based constitutive model of dislocation glide in metals that explicitly accounts for the redistribution of dislocations due to their motion. The model parameterizes the
complex microstructure by dislocation densities of edge and screw character, which either occur with monopolar properties, i.e. a single dislocation with positive or negative line sense, or with
dipolar properties,
i.e. two dislocations of opposite line sense combined. The advantage of the model lies in the description of the dislocation density evolution, which comprises the usual rate equations for
dislocation multiplication and annihilation, and formation and dissociation of dislocation dipoles. Additionally, the spatial redistribution of dislocations by slip is explicitly accounted for. This
is achieved by introducing an advection term for the dislocation density that turns the evolution equations for the dislocation density from ordinary into partial
differential equations. The associated spatial gradients of the dislocation slip render the model nonlocal. The model is applied to wedge indentation in single-crystalline nickel. The simulation
results are compared to published experiments (Kysar et al., 2010) in terms of the spatial distribution of lattice rotations and geometrically necessary dislocations. In agreement with
experiment, the predicted dislocation fluxes lead to accumulation of geometrically necessary dislocations around a vertical geometrical border with a high orientation gradient
below the indenter that is decisive for the overall plastic response. A local model variant without dislocation transport is not able to predict the influence of this geometrical transition zone
correctly and is shown to behave markedly softer.
Strain rate dependency of dislocation plasticity
Dislocation glide is a general deformation mode, governing the strength of metals. Via discrete dislocation dynamics and molecular dynamics simulations, we investigate the strain rate and dislocation density dependence of the strength of bulk copper and aluminum single crystals. An analytical relationship between material strength, dislocation density, strain rate and dislocation mobility is proposed, which agrees well with current simulations and published experiments. Results show that material strength displays a decreasing regime (strain rate hardening) and then increasing regime (classical forest hardening) as the dislocation density increases. Accordingly, the strength displays universally, as the strain rate increases, a strain rate-independent regime followed by a strain rate hardening regime. All results are captured by a single scaling function, which relates the scaled strength to a coupling parameter between dislocation density and strain rate. Such coupling parameter also controls the localization of plasticity, fluctuations of dislocation flow and distribution of dislocation velocity.