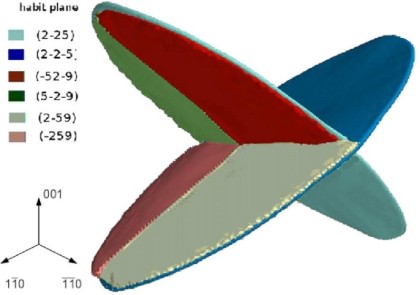
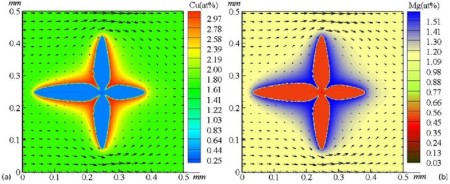
Phase field modeling

When a homogeneous, single-phase, binary solution is rapidly quenched from a sufficiently elevated homologous temperature to a temperature below its upper critical solution temperature, gradual phase separation may occur. However, phase transition will only happen if the quench brings the solution into the two-phase coexistence region and if the temperature suffices for diffusion. Phase separation may proceed through the discontinuous process of nucleation and growth in the metastable region, or by the continuous process of spinodal decomposition in the unstable region (Cahn and Hilliard 1971; Wagner and Kampmann 1991). While small concentration fluctuations in the metastable region increase the total free energy of the system in terms of the nucleation energy, a sufficiently large but finite concentration (concentration in the precipitate) perturbation can degrade it. This renders the entire solid solution unstable and leads to phase separation by discontinuous nucleation and subsequent growth. In contrast, continuous phase separation, as described by spinodal decomposition, gradually degrades the free energy right from the beginning of phase transition, i.e. it is a non-activated process and does not reveal any threshold energy. Such coherent, i.e. isostructural, decomposition phenomena are theoretically described by the Cahn–Hilliard model (1958), which combines the generalized law of diffusion with a Landau energy term.  The extension of the original Cahn–Hilliard model to non-coherent phase transformations, i.e. transitions which change the long-range order, the crystal orientation, or the crystal structure, is provided by the Allen–Cahn model (1979) and its generalized derivatives. While the Cahn–Hilliard model describes the kinetics of transformation phenomena with conserved field variables (e.g. chemical concentration), the Allen–Cahn model describes transformations with nonconserved variables (e.g. long-range order). The Ginzburg–Landau and Cahn–Hilliard-type kinetic phase field models represent a group of very general and flexible phenomenological continuum field approaches which are capable of describing continuous and quasi-discontinuous phase separation phenomena in coherent and incoherent systems at the nanoscopic and mesoscopic level. While original versions of the Ginzburg–Landau approach addressed electromagnetic problems with nonconserved field variables, such as phase separation phenomena in Shubnikov phases, i.e. the concentration distribution of Cooper pairs, advanced metallurgical variants are capable of addressing the distribution of conserved continuous atomic concentration parameters and nonconserved quasi-discontinuous structural and/or orientational parameters in coherent and non-coherent systems. Phase field models can be regarded as a set of Onsager kinetic equations furnished with an appropriate free energy functional that may depend on such quantities as atomic or boson concentration and long-range order. For transcribing this approach into a form that is discrete in space, these state parameters are used as field variables. The dependence of the variables on the spatial coordinates enables one to prescribe heterogeneous composition and structure fields, and allows one to simulate both the kinetics and the resulting morphology of phase separation phenomena. Phase field approaches are generally based on the assumption that the material is homogeneous and that the chemical portion of the total free energy density functional can be expressed in a Landau form. In those versions where only the conservative concentration field is considered (original Cahn–Hilliard theory), the phase field method is confined to describing isostructural phase transformations. The phases may then differ from each other only in concentration, but not in long-range order or crystal structure. For incorporating the latter parameters, the theory can be extended by introducing additional, nonconservative field variables (Allen–Cahn theory) and by complementing the energy density functional with corresponding terms. 

The conventional reduction of iron oxide ores with carbon-carriers (mostly through coke) is one of the largest sources of greenhouse gas emissions in the industry. This motivates global efforts to replace the coke-based blast furnace reduction by hydrogen-based direct reduction (HyDR). Iron oxide reduction with
hydrogen has been widely investigated both experimentally and theoretically as an alternative approach. The HyDR process includes multiple types of chemical reactions, solid state and defect-mediated diffusion (of oxygen and hydrogen species), several phase transformations, as well as massive volume shrinkage and mechanical stress buildup. However, studies focusing on the  chemomechanical interplay during the reduction reaction inƒuenced by microstructure are sparse.
We have now introduced a chemo-mechanically coupled phase-field (PF) model has been developed to explore the interplay between phase transformation, chemical reaction, species diffusion, large elasto-plastic deformation and microstructure evolution. Energetic constitutive relations of the model are based on the system free energy which is calibrated with the help of a thermodynamic database.

The phase field model has been in a first approach applied to the classical core-shell (wüstite-iron) structure. Simulations show that the phase transformation from wüstite to -iron can result in high stresses and rapidly decelerating reaction kinetics. Mechanical stresses create elastic energy in the system, an effect which can negatively influence the phase transformations, thus causing slow reaction kinetics and low metallization. However, if the elastic stress becomes comparatively high, it can shift the shape of the free energy from a double-well to a single-well case, speed up the transformation and result in a higher reduction degree compared to the low-stress double-well case. The e model has been
applied to simulate an experimentally characterized iron oxide specimen with its complex microstructure. The observed microstructure evolution during reduction is well predicted by the model. The simulation results also show that isolated pores in the microstructure are filled with water vapor during reduction, which can influence the local reaction atmosphere and dynamics.