Modelign of Green Steel Production by Hydrogen-based Direct Reduction considering Thermodynamics and Microstructure

Direct reduction of iron involves complex, multiscale phenomena, encompassing 
solid-state phase transformations and gas transport through pores that must be 
accurately represented for predictive industrial implementation. Here, we present a thermodynamically sound pellet-scale model that describes these mechanisms and can serve as a foundation for improving the understanding of pellet reduction kinetics in H2/CO-containing atmospheres. The model assumes that the gas phase remains in thermodynamic equilibrium instantly adjusting to any changes in composition. This reduces the number of fitting parameters drastically compared to other existing models, while maintaining a strict thermodynamic upper bound estimate. A driving force term is included in the reaction rate equation ensuring that the three iron oxide reduction steps and the formation of graphite and cementite in carbon-containing gases occur only if they are thermodynamically possible. It is demonstrated that fitting kinetic parameters based on conversion degree data alone leads to overfitting. This is true both for existing models and the model introduced here, despite the fact that the latter contains fewer parameters. To overcome this overfitting problem, spatially resolved microstructural data at key reduction stages can be considered, as shown here for recently reported data for a pellet reduced in H2 atmosphere.

I. Introduction to the Modeling of Direct Rediction of Iron Ores  with Hydrogen and the Problem of Overfitting in Direct Reduction Kinetics

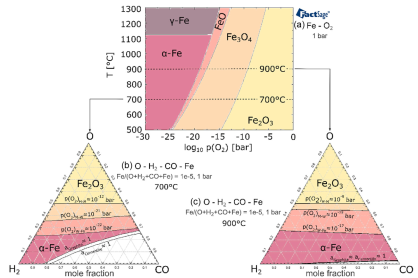
The direct reduction of iron (DRI) pellets is a critical, multi-stage chemical process in steel production, gaining increasing importance as the industry transitions toward decarbonized processes utilizing and $CO$ atmospheres. Accurately modeling the kinetics of this process is essential for industrial optimization and control. However, the reduction of iron ore is inherently complex, involving multiscale phenomena that occur simultaneously: gas transport (diffusion) through the pellet's porous structure, solid-state phase transformations (reduction of hematite, ${\mathrm{Fe}}^2{\mathrm{O}}^3$, to magnetite, ${\mathrm{Fe}}^3{\mathrm{O}}^4$, to wüstite, $\mathrm{FeO}$, and finally to metallic iron, $\mathrm{Fe}$), and chemical reaction kinetics at the phase boundaries.

Existing pellet reduction models, often semi-empirical, have conventionally struggled with a major statistical pitfall: overfitting. These models typically rely on fitting a large number of adjustable kinetic parameters to macroscopic data, specifically the overall degree of conversion versus time. While such models can perfectly replicate experimental conversion curves, the resulting fitted parameters often lack physical meaning, are not unique, and, crucially, fail to predict the behavior of the system under slightly different conditions (e.g., varying temperature, gas composition, or pellet size). This lack of physical grounding makes them unreliable for industrial prediction and scale-up.

The paper, by Büyükuslu et al., addresses this fundamental limitation by proposing a novel, thermodynamically constrained, pellet-scale reduction model. The primary goal is to drastically reduce the number of phenomenological fitting parameters while ensuring the model remains strictly adherent to the laws of physical chemistry, thereby mitigating overfitting and improving true predictive power.

II. Thermodynamically Sound Model Formulation

The core innovation of the presented model lies in its rigorous integration of thermodynamics into the reaction rate equation. This approach provides a level of internal physical consistency often missing in purely kinetic or empirical models.

Gas Phase Equilibrium and Parameter Reduction: The authors introduce a significant simplification that serves as the main mechanism for parameter reduction: the assumption that the gas phase within the porous structure remains in instantaneous thermodynamic equilibrium. While in reality, the gas phase might experience local gradients, this assumption is leveraged to establish a strict upper bound on the reduction rate. By fixing the gas composition based on equilibrium calculations at any point in the pellet, the number of independent kinetic parameters required to describe the gas-solid reactions is substantially decreased compared to models that must track and fit parameters for complex non-equilibrium gas-phase reactions.

The Role of Thermodynamic Driving Force ($DF$): Crucially, the reaction rate equation is modified to include a thermodynamic driving force term, $DF$. This term is directly derived from the Gibbs free energy change ($\Delta G$) of the reaction. The introduction of $DF$ serves as a physically-based gatekeeper for the entire process: a reaction, whether it be one of the three iron oxide reduction steps or the precipitation of carbon phases (graphite or cementite) from $CO$ (Boudouard reaction), can only proceed if it is thermodynamically possible (i.e., $\Delta G<0$, or $DF>0$).

The inclusion of the $DF$ term ensures that the calculated reaction rate is always bounded by the thermodynamic limit, meaning the model cannot predict unrealistic reaction advancement simply by adjusting kinetic parameters. This provides a rigorous, non-negotiable physical constraint on the model's behavior. The reaction rate, $R$, is generally expressed as a function of the kinetic constant, $k$, and the driving force, $DF$, preventing the system from evolving beyond its stable thermodynamic state.

III. Addressing Multiscale Phenomena: Microstructure and Transport

While the thermodynamic constraints anchor the model in physical reality, the model must also account for the complex, multiscale phenomena involved in pellet reduction. The reduction process is governed not only by chemical kinetics but also by the transport of gaseous species through the evolving microstructure of the pellet.

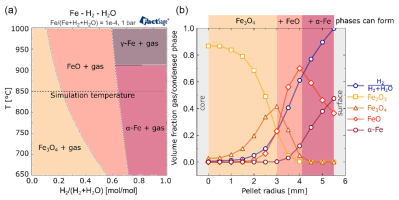
Modeling Gas Transport: The model incorporates the principles of gas diffusion and convection through porous media. As reduction proceeds, the internal structure of the pellet undergoes massive change: porosity increases significantly as oxygen is removed, and the solid phases (hematite, magnetite, wüstite, and iron) transform. The model must track how these microstructural changes—specifically the local porosity, pore size distribution, and tortuosity (the winding path gas must follow)—influence the effective diffusivity of the reducing gas ($H^2$ and $CO$) and the product gas ($H^{2}O$ and $C{O}^2$). This dynamic coupling between the reaction progress and the changing internal pellet geometry is what links the "microstructure" concept to the kinetic model.

The explicit coupling of the model to microstructural parameters ensures that the predicted reaction rate gradient across the pellet (e.g., faster reduction at the surface, slower at the core) is a result of physically relevant transport limitations, not just arbitrary kinetic constants.

IV. IMposing Physical Constraints in Direct Reduction Models

The paper’s central contribution is the demonstration that fitting parameters solely to macroscopic conversion curves inevitably leads to overfitting, even for a thermodynamically constrained model. The authors show that multiple distinct sets of fitted kinetic parameters can produce near-identical overall conversion curves, yet these parameter sets represent vastly different underlying physical behaviors (e.g., local phase compositions or reaction front velocities within the pellet).

Therefore, the only true way to mitigate overfitting and achieve a physically predictive model is to constrain the model using multiscale data. The strength of the presented model is its readiness to be validated not only against overall conversion data but, critically, against microstructural and local chemical information. This includes experimental measurements of local gas compositions, internal phase boundaries, and spatial distribution of phase fractions (which can be obtained via techniques like X-ray tomography or SEM/EDX analysis).

In summary, the work provides a robust and elegant framework for modeling iron pellet reduction. By anchoring the chemical transformation steps to a rigorous thermodynamic driving force and simultaneously accounting for the evolving microstructure's impact on gas transport, the model successfully shifts the paradigm from purely phenomenological fitting to physically constrained prediction. This is a crucial step for developing accurate, reliable models necessary for optimizing the energy efficiency and carbon footprint of future direct reduction technologies.

This draft is appropriate for an advanced undergraduate or graduate-level engineering or materials science course. Let me know if you'd like to dive deeper into the specifics of the diffusion equations or explore the implications of using this model for predicting graphite formation in carbon-containing gases.