Crystal plasticity phase field multiphysics simulation
Why combining chemistry and mechanical modeling in microstructure and materials research?
One purpose of metallurgical and materials science is the theory-guided tailoring of materials, including elasto-plastic mechanical response, chemical composition and microstructure, in order to obtain improved properties for a sustainable technological development.
Considering both, mechanics and chemistry in materials with complex microstructures enables to predict their properties and helps to design digital twins of processes and materials.
While there has been an immense growth over recent years in the use of (often freely available) modelling and simulation tools towards this goal, the realistic prediction of the thermo-chemo-mechanical interactions relevant to industrial processes is still a key development required to enable technological advances in material design, manufacturing and product development for harsh-service environments.
In that context particularky the interaction of solute diffusion and elasto-plastic deformation plays a prominent role in the microstructural evolution and the subsequent performance, be it for metallic sheet products, batteries during charging or recharging or the thermo-chemo-mechanical interplay in the compounds serving in computer chips.
What is the next step in the development of phase field models for coupling mechanics, temperature and chemistry in materials modeling?
The phase-field method is particularly well-suited to model coupled mechanical-thermal-chemical microstructure evolution and structure-property relations.
It has been successfully applied to model multiple thermo-chemo-mechanical processes including solidification, precipitation, fracture and dislocation motion.
Further methodological developments including chemo-mechanical interface modelling and homogenisation have also been treated.
However, the majority of chemo-mechanical phase-field modeling studies are limited to linear elastic mechanics.
Until very recently, only few works have been carried out to fully couple the chemo-elasto-plastic processes in a thermodynamically consistent framework.
The use of diffuse-interface models to describe interfacial phenomena dates back to Cahn and Hilliard, and further to Ginzburg and Landau.
The original Cahn–Hilliard equation was used to model spinodal decomposition in binary alloys, but has since been extended to multi-component systems and coupled with microelasticity.
A critical challenge in simulating the thermodynamics of multi-component chemo-mechanical systems is the numerical approximation
of a generally non-convex chemical free energy.
Several numerical methods have been developed to solve non-convex systems using finite difference, mixed finite element with composition and chemical potential treated as independent fields,
isogeometric and spectral spatial discretisations.
In the context of numerical time-integration, the stability, robustness and efficiency of the resulting solution algorithm is sensitive to the degree of non-convexity of the chemical free
energy.
A practical and quite successful approach in this regard is the splitting of the chemical free energy into concave and convex components, which are then approximated separately.
In particular, splitting methods have recently been applied to the multi-component, multi-phase Cahn–Hilliard equation with a generalised non-convex Landau energy landsacpe.
In the context of a mixed finite-element-based weak formulation of the classic Cahn–Hilliard relation, Gomez and Hughes employed a chemical energy splitting approach based on the sign of the fourth-order derivatives of the underlying energy functional. A recent mixed weak formulation of chemo-mechanics for two-phase, two-component finite-deformation gradient elastic solids based on unconditionally stable, second-order accurate time-integration and Taylor expansion of the non-convex energy has been given by Sagiyama et al..
More recently, starting from a grand potential functional, the transport relations have been formulated for multi-component and multi-phase systems.
In such an approach, the thermodynamics of the system is set in a grand canonical ensemble and formulated in terms of the chemical potential. As a result, boundary and interface conditions based
on the chemical potential, needed for a realistic representation of macroscopic systems where the total number of particles cannot be fixed, are naturally incorporated. However, these approaches are
based on a Legendre transformation, which does not exist for more general non-convex forms of the chemical free energy.
In our approach, a convex splitting of the chemical free energy is instead used to invert the multi-component chemical potential–composition relation.
This results in an expression for component transport in terms of the chemical potential rather than the chemical composition, analogous to the grand potential approach, but applicable to more
general forms of the chemical free energy.
Comput. Methods Appl. Mech. Engrg. 365 (2020) 113029
2020 Multi-component chemo-mechanics bas[...]
PDF-Dokument [3.1 MB]
Introduction to the crystal plasticity method
Crystal plasticity modeling methods (CP) are continuum field approaches for the simulation of elastic-plastic material deformation where the underlying elementary shear carriers such as dislocations or twins follow tensorial kinematics.
Deformation resistance on each of these discrete shear systems is often described in terms of material- and defect specific self-hardening and latent hardening laws.
The resulting differential equations can be solsved using homogenization models, the finite element method or FFT based spectral solvers.
Results of such simulations are stresses, strain, crystallographic textures as well as detailed insights on the activated deformation systems and collective effects at a grain and subgrain scale.
Introduction to the phase field method
The phase field method applies diffusion-type kinetic evolution equations to Landau-type energy landscapes. It is derived from the time dependent Ginzburg-Landau equation and can be applied to conserved as well as to not conserved field variables which may either represent atomic species or microstructural phases or crystals.
Projects where we combine crystal plasticity with phase field simulations to simulate coupled chemo-structural-mechanical problems
Elasto-viscoplastic phase field modelling of anisotropic cleavage fracture
J. Mech. Phys. Solids 99 (2017) 19–34
JMPS 2017 Elasto-viscoplastic phase fiel[...]
PDF-Dokument [1.4 MB]
A finite-strain anisotropic phase field method is developed to model the localisation of damage on a defined family of crystallographic planes, characteristic of cleavage fracture in metals.
The approach is based on the introduction of an undamaged configuration, and the inelastic deformation gradient mapping this configuration to a damaged configuration is
microstructurally represented by the opening of a set of cleavage planes in the three fracture modes. Crack opening is modelled as a dissipative process, and its evolution is
thermodynamically derived. To couple this approach with a physically-based phase field method for brittle fracture, a scalar measure of the overall local damage is introduced, whose
evolution is determined by the crack
opening rates, and weakly coupled with the non-local phase field energy representing the crack opening resistance in the classical sense of Griffith. A finite-element implementation of
the proposed model is employed to simulate the crack propagation path in a laminate and a polycrystalline microstructure. As shown in this work, it is able to predict the localisation
of damage on the set of pre-defined cleavage planes, as well as the kinking and branching of the
crack resulting from the crystallographic misorientation across the laminate boundary and the grain boundaries respectively.
A phase-field model for incoherent martensitic transformations including plastic accommodation processes in the austenite
Journal of the Mechanics and Physics of Solids 59 (2011) 2082–2102
phase-field-model-martensitic-transforma[...]
PDF-Dokument [1.4 MB]
A phase field model for damage in elasto-viscoplastic materials
Comput. Methods Appl. Mech. Engrg. 312 (2016) 167–185
phase field damage elasto-viscoplastic m[...]
PDF-Dokument [2.3 MB]
A phase field method for brittle fracture is formulated for a finite strain elasto-viscoplastic material using a novel obstacle phase field energy model. The obstacle energy model results in
a crack profile with compact support, and thus gives a physically realistic description of the material behaviour at the vicinity of the crack tip. The resulting variational inequality is
discretised by a finite element method, and is efficiently solved using a reduced space NEWTON method. The solution accuracy and numerical performance of this method is compared with a
conventional phase field energy model for brittle fracture through representative
examples, and a significant reduction in the numerical solution cost is demonstrated.
Coupled Crystal Plasticity–Phase Field Fracture Simulation Study on Damage Evolution Around a Void: Pore Shape Versus Crystallographic Orientation
JOM, Vol. 69, No. 5, 2017
Crystal Plasticity Phase Field Fracture [...]
PDF-Dokument [987.3 KB]
Various mechanisms such as anisotropic plastic flow, damage nucleation, and
crack propagation govern the overall mechanical response of structural materials. Understanding how these mechanisms interact, i.e. if they amplify mutually or compete with each other, is
an essential prerequisite for the design of improved alloys. This study shows—by using the free and open source software DAMASK (the Dusseldorf Advanced Material Simulation Kit)—how the
coupling of crystal plasticity and phase field fracture methods can increase the understanding of the complex interplay between crystallographic orientation and the geometry of a void. To
this end, crack initiation and propagation around an experimentally obtained pore with complex shape is investigated and compared to the situation of a simplified spherical void. Three
different crystallographic orientations of the aluminum matrix hosting the defects are considered. It is shown that crack initiation and propagation depend in a non-trivial way on
crystallographic orientation and its associated plastic behavior as well as on the shape of the pore.
Constitutive modeling of strain induced grain boundary migration via coupling crystal plasticity and phase-field methods
International Journal of Plasticity 99 (2017) 19
IJP 2017 crystal plasticity and phase-fi[...]
PDF-Dokument [1.8 MB]
In this project we used a thermodynamically consistent finite-deformation-based constitutive theory to describe strain induced grain boundary migration due to the heterogeneity of stored deformation energy in a plastically deformed polycrystalline cubic metal. Considering a representative volume element, a mesoscale continuum theory is developed based on the coupling between dislocation density-based crystal plasticity and phase field methods. Using the Taylor model-based homogenization method, a multiscale coupled finite-element and phase-field staggered time integration procedure is developed and implemented into the Abaqus/Standard finite element package via a user-defined material subroutine. The developed constitutive model is then used to perform numerical simulations of strain induced grain boundary migration in polycrystalline tantalum. The simulation results are shown to qualitatively and quantitatively agree with experimental results.
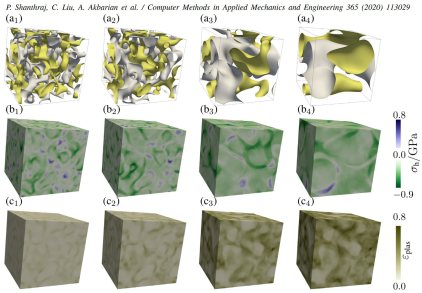
Analysis of strain and stress partitioning in bainitic steels with martensite–austenite constituents using crystal plasticity multiphysics simulations
Dual phase steels with microstructures based on bainite as a matrix together with dispersed martensite-austenite (MA) constituents provide the ingredients required for the improvement of the strain capacity and toughness of bainite steels. To fine-tune the alloy design and ensure such novel dual-phase steels have the required mechanical properties, better understanding of the governing deformation micromechanisms is essential. For this purpose, a recently developed joint numerical-experimental approach that involves the integrated use of microscopic digital image correlation analysis, electron backscatter diffraction, and multiphysics crystal plasticity simulations with a spectral solver can be employed. The local strain and stress evolution and microstructure maps of representative microstructural patches were here captured with a high spatial resolution using this approach. A comparison of these maps provides new insights into the deformation mechanism in dual-phase microstructures, especially regarding the influence of the bainite and martensite-austenite grain size and the martensite-austenite distribution on the strain localization behavior.
International Journal of Plasticity
Volume 104, May 2018, Pages 39-53
IJP 2018 strain stress partitioning in b[...]
PDF-Dokument [3.6 MB]