Lattice Boltzmann models for nano- and microscale fluid dynamics
What is lattice Boltzmann method for fluid dynamics?
The lattice Boltzmann model is a powerful technique for the simulation of single and multi-phase flows in complex geometries. Owing to its excellent numerical stability and constitutive versatility it can play an essential role as a simulation tool for understanding advanced materials and processes. Unlike conventional continuous-field Navier–Stokes solvers, lattice Boltzmann methods consider flows to be composed of a collection of pseudo-particles that are represented by a velocity distribution function. These fluid portions reside and interact on the nodes of a grid. System dynamics and complexity emerge by the repeated application of local rules for the motion, collision and redistribution of these coarse-grained droplets. The lattice Boltzmann method, therefore, is an ideal approach for mesoscale and scale-bridging simulations. It is capable to tackling particularly those problems which are ubiquitous characteristics of flows in the world of materials science and engineering, namely, flows under complicated geometrical boundary conditions, multi-scale flow phenomena, phase transformation in flows, complex solid–liquid interfaces, surface reactions in fluids, liquid–solid flows of colloidal suspensions and turbulence. Since the basic structure of the method is that of a synchronous automaton it is also an ideal platform for realizing combinations with related simulation techniques such as cellular automata or Potts models for crystal growth in a fluid or gas environment.
Approaches to computational fluid dynamics together with their preferred range of applicability. Molecular dynamics methods integrate Newton’s equations of motion for a set of molecules on the basis of an intermolecular potential. Dissipative particle dynamics and direct simulation Monte Carlo are off-lattice pseudo-particle methods in conjunction with Newtonian dynamics. Lattice gas and lattice Boltzmann methods treat flows in terms of coarse-grained fictive particles which reside on a mesh and conduct translation as well as collision steps entailing overall fluid-like behaviour. Navier–Stokes approaches solve continuum-based partial differential equations which account for the local conservation of mass, momentum and energy. These three methods have their respective strengths at different Knudsen numbers, where the Knudsen number is the ratio between the mean free molecule path and a characteristic length scale representing mesoscopic system heterogeneity (e.g. the obstacle size). (Ref.: Raabe; Modelling Simul. Mater. Sci. Eng. 12 (2004) R13–R46).
Overview of the lattice Boltzmann method for
nano- and microscale fluid dynamics in materials science and engineering
Modelling Simul. Mater. Sci. Eng. 12 (20[...]
PDF-Dokument [995.4 KB]
Why use discrete methods in computational fluid mechanics?
The theoretical picture of fluid dynamics in the materials engineering community largely departs from the work of Navier and Stokes from the first half of the 19th century.
Their differential formulation of the mechanics of incompressible flows, the so-called Navier–Stokes equation, accounts for the conservation of mass, momentum and energy, and the
requirement that these quantities be conserved locally. Tackling hydrodynamics and related problems with this equation amounts to solving coupled sets of nonlinear partial differential
field equations by use of finite difference or finite element methods. Although the Navier–Stokes framework serves as a long-established basis for predicting fluid behaviour, it has
still not been possible to resolve some basic questions in the fields
of modern materials science and engineering with it. This is due to the fact that the Navier–Stokes differential formulations theoretically do not apply and numerically also do not
converge under conditions which are characterized by large Knudsen numbers (mean free molecule path divided by characteristic system length). Such restrictions occur when the mean free
path of the fluid molecules is similar to the geometrical system constraints, such as, for instance
the obstacle spacing or the roughness wavelength which may characterize mesoscopic system heterogeneity.
Prominent examples where such limitations occur are the simulation of nano- and microflows in filters, foams, micro-reactors or otherwise confined geometries; multicomponent flows in the
area of polymer and metal processing; tribology and wear in the area of lubricated contact mechanics and metal forming; liquid crystal processing; nanoscale process technology; lubrication
in miniaturized components, liquid phase separation; joint fluid–gas flows; abrasion and sedimentation; fluid percolation in cellular structures; processing of
metallic foams; as well as corrosion and solidification in non-quiescent environments to name but a few. These examples do not only challenge our basic understanding of fluid mechanics but
represent at the same time key issues in modern materials science and engineering of considerable practical relevance. Lattice gas cellular automata and their more mature (non-Boolean)
successors, the lattice Boltzmann automaton techniques are predestined to tackle some of these challenges in the domain of materials-related computational fluid dynamics in a more
efficient way than the conventional Navier–Stokes approach. The lattice Boltzmann technique belongs to a broader group of pseudo-particle methods which form a growing class of multi-scale
simulation approaches to computational fluid mechanics. Other important particle-based approaches in this class are (besides lattice gas cellular automata) the dissipative particle dynamics
method and the direct simulation Monte Carlo method together with its hybrid mesh refinement variations.
These pseudo-particle approaches can be grouped into lattice-based cellular automaton approaches (lattice gas method, lattice Boltzmann method) and off-lattice approaches (dissipative
particle dynamics method, direct simulation Monte Carlo method). While the reminder of this overview deals exclusively with vectorial cellular automaton models of fluid flow, the ensuing
section provides a concise summary of the off-lattice methods.
What is a lattice gas cellular automaton technique?
Lattice gas cellular automata with Boolean particle states residing on fixed nodes were suggested by Frisch, Hasslacher and Pomeau in 1986 (FHP lattice gas model) for the reproduction of
Navier–Stokes dynamics. A previous formulation for vector automata was already in 1973 suggested by Hardy, Pomeau and de Pazzis (HPP lattice gas model). However, this earlier version of a
lattice gas method was based on a square grid and could, therefore, not fulfill the requirement of rotational invariance. The FHP lattice gas model published later used a hexagonal
two-dimensional lattice which fulfills both, conservation
of particle number and rotational invariance. All particles in a Boolean lattice gas have the same unit mass and the same magnitude of the velocity vector. The model imposes, as an
exclusion principle, that no two particles may sit simultaneously on the same node if their direction is identical. For the square lattice originally suggested by the HPP model, this
implies that there can be at most four particles per node. This occupation principle, originally meant to permit simple computer codes, has the consequence that the equilibrium distribution
of the particles follows a Fermi–Dirac distribution. Motion of the particles consists of moving them from one lattice node to their nearest neighbour in
one discrete unit of time according to their given unit momentum vector. The evolution of
system dynamics of the lattice gas takes place in four successive steps. The first one is the advection or propagation step. It consists of moving
all particles from their
nodes to their nearest neighbour nodes in the directions of their respective velocity vectors. The second one is the collision step. It is conducted in such a way that
interactions between particles arriving at the same node coming from different directions take place in the form of local instantaneous collisions. The elastic collision rules conserve both
mass and momentum. This implies that particles arriving at the same node may exchange momentum if it is compatible with the imposed invariance rules. The third step is (usually) the
bounceback
step. It imposes no-slip boundary conditions for those particles which hit an obstacle. The fourth step updates all sites. This is done by synchronously mapping the new particle coordinates
and velocity vectors obtained from the preceding steps onto their new positions. Subsequently the time counter is increased by one unit. Owing to the discrete treatment of the
pseudo-particles and the discreteness of the collision rules Boolean lattice gas automata reveal some intrinsic flaws such as the violation of Galilean invariance1 and the occurrence of
large fluctuations. The latter disadvantage can to a certain extent be circumvented by introducing localized averaging procedures where a group of neighbouring vectors is summarized into a
coarse-grained net-vector.
What is a differemce between the lattice gas method and the lattice Boltzmann approach?
The lattice Boltzmann approach has evolved from the lattice gas models in order to overcome the shortcomings discussed above. It corresponds to a space-, momentum- and
time-discretized version of the Boltzmann transport equation. The main rationale behind the introduction of the lattice Boltzmann automaton is to incorporate the physical nature of fluids
from a more statistical standpoint into hydrodynamics solutions than in the classical lattice gas method. According to the underlying picture of the Boltzmann transport equation the idea of
the lattice Boltzmann automaton is to use sets of particle velocity distribution functions instead of single pseudo-particles and to implement the dynamics directly on those average values.
The particle velocities in the lattice Boltzmann scheme are not Boolean variables as in conventional lattice gas automata, but real-numbered quantities as in the Boltzmann transport
equation. This means
that Fermi-like statistics no longer apply. It is also important to note that in contrast to the conventional lattice gas method the lattice Boltzmann approach may use pseudo-particles
with zero velocity. These are required for simulating compressible hydrodynamics by using a tunable model sound speed. Another main difference between the original lattice gas and the
lattice Boltzmann methods is the fact that the former approach quantifies the particle interactions in terms of discrete local Boolean redistribution rules (collision rules) while the
latter approach conducts (non-Boolean) redistributions of the particle velocity distribution (relaxation rules, collision operator).
The main advantage of the lattice Boltzmann method compared to the original lattice gas is that small sets of neighbouring nodes in a Boltzmann lattice are capable of creating smooth flow
dynamics as opposed to the lattice gas methods which entail rather coarse dynamical behaviour. This means that the Boltzmann method requires less averaging and provides increased
performance.
Lattice Boltzmann modeling of dendritic growth in a forced melt convection
Acta_Materialia_2009_vol_57_page_1755_LB[...]
PDF-Dokument [1.0 MB]
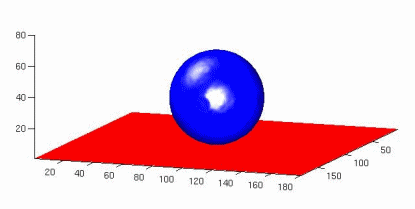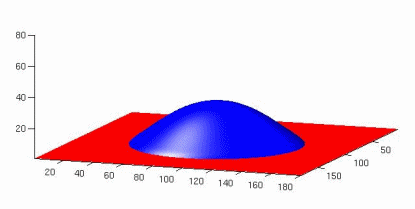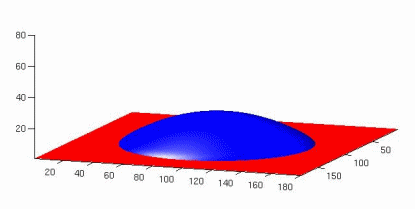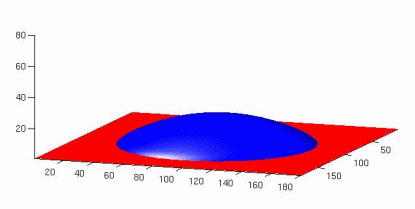
droplets on rough hydrophobic substrates[...]
PDF-Dokument [452.1 KB]
Phys-Rev-e051606-Small droplets on super[...]
PDF-Dokument [3.2 MB]