Multiscale Modeling of Materials

Multi-scale and multi-physics materials modeling combines existing and emerging methods from diverse scientific disciplines to bridge the wide range of time and length scales that are inherent in a number of essential phenomena and processes in materials science and engineering.

Currently we can observe how novel developments have changed the field in recent years from a descriptive to a predictive approach and have led to the modeling of properties and functions of complex materials under realistic constraints. A proper linkage of electronic-structure theory and statistical methods is necessary to describe the physics and chemistry that govern the properties and processes of materials under realistic temperature and pressure conditions.

Multi-Scale and multiphysics models can be used along very different research and engineering directions.
The most prominent field of multiscale materials modeling lies in predicting relations between structure, processing amd properties of complex materials beyond the regimes that have been probed experimentally.
Another important field of high interest in that context lies in the use of models for predicting so far unknown materials structures, properties or performance. 
The third essential field lies in developing adequate multiscale models that can be used for process simulation, in the best case even for online structure - property predictions of materials during manufacturing.

In our daily life, we are confronted by a multitude of materials-related phenomena whose essential role often extends over many scales in time and space.
One example found at the very basis of life is protein folding. In this process polypeptides fold into their characteristic 3D structure from an originally random coil. For most proteins this structuring is essential to their function. While protein folding requires up to several minutes, the underlying chemical rearrangements take place within picoseconds through van der Waals and hydrogen bonds.
In materials engineering, corrosion of metals is an essential process that destroys goods worth many billions of Euro every year. Beyond the purely monetary value, corrosion profoundly affects the safety of advanced products and processes, whose integrity and functionality society relies upon in fields such as energy, transportation, and information. While single electron transfer at a metallic surface occurs within femtoseconds and multiple oxide layers require minutes to form via diffusion and multiple reaction cascades, the macroscopic corrosion and decomposition of metallic structures proceeds over decades and even over hundreds of years.
In either case, be it the foundation of living matter and biological information or the engineering design of advanced materials, products and processes, the underlying phenomena span a huge and hierarchically organized sequence of time and length scales.
Describing, understanding, and finally quantitatively predicting such multiscale and multiphysics phenomena using advanced theoretical methods is a grand scientific task that is key to assuring the safety and well-being of our modern society.
Recently we observe how novel developments have changed the field of multiscale modeling in recent years from a descriptive to a predictive method for modeling of properties and functions of materials and processes.
The greatest progress that has been achieved in this field in recent years lies in the closer linkage of electronic-structure, statistical, and mean-field theory. The joint application of these formerly isolated methods is absolutely necessary to describe the physics and chemistry that govern the properties and processes of materials under realistic temperature and loading conditions on these vastly diverging scales.
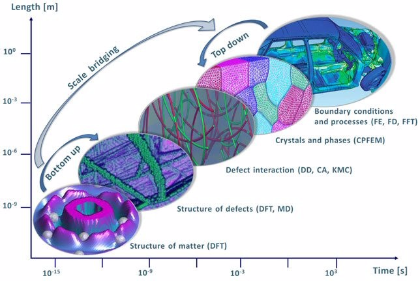
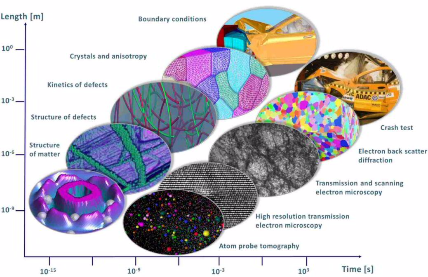
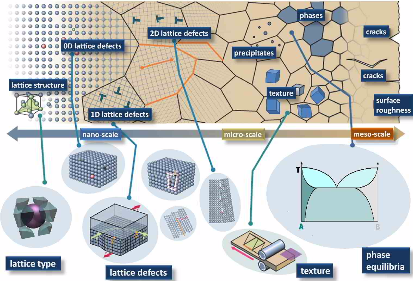
Typical examples at the small scale are ab initio methods (many-body electronic structure theory, density functional theory, quantum chemistry). These approaches are vital for successful multiscale models as they alone can elucidate the nature of the bonds and elementary excitations from which all material properties derive, Fig. 1. Above the scale of electrons, atomistic dynamics and statistics are widely used (referred to as molecular dynamics or kinetic Monte Carlo models). They are particularly suited to understand kinetically dominated mechanisms. At the mesoscopic scale, mean field rate theoretical methods are in use that typically mimic average dynamical properties (Master equations, Langevin equations). Also automaton models (lattice gas, cellular automata) and pseudo-particle dynamical approaches occur at that scale. Finally, continuum-based thermodynamics or constitutive kinetic models (phase field, Navier-Stokes) that are typically solved using variational methods serve at mesoscopic and macroscopic scales.
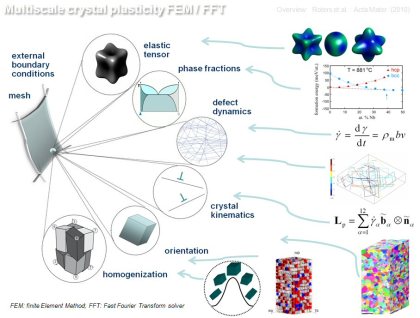
As numerical solvers typically Finite Element, Fast Fourier, or Finite Difference methods are used. These do not represent models themselves but allow modelers to obtain efficient solutions to the underlying coupled sets of partial differential equations that describe the system.

Multiscale Modeling of Materials in the Max-Planck Society