Yield Surface Simulation

A yield surface is a generalized form of the yield strength, at which materials start to undergo inelastic deformation (also, more correctly, referred to as elastic-plastic deformation).   It can be understood in terms of two main features  associated with the plastic deformation of materials.

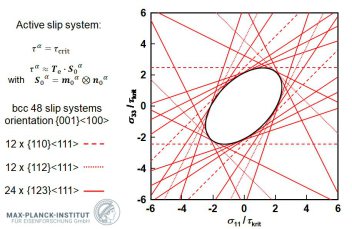
The first observation is that practically all materials deform differently when mechanically loaded in different directions.   This means that the well-known stress-strain curves that are used to describe the change in stress as a function of deformation must be regarded as simple one-dimensional sections through a 6-dimensional portion of the stress space ( when considering also the effect of hydrostatic components).  The second observation which helps to understand this phenomenon lies  in analysing the plastic deformation of single crystalline materials.  When conducting such deformation experiments  it becomes quickly apparent that most materials have preferred atomistic deformation mechanisms that are confined to certain crystallographic directions and planes.  This reveals the atomic nature of such directional dependence which is generally also referred to as anisotropy.

Yield surface functions are typically mathematical descriptions of such higher dimensionality of the inelastic flow of materials.  They can be formulated based on empirical equations that match the observed anisotropy ( directional dependence) in the  materials' plastic flow or they can be derived from the atomistic nature the underlying physical mechanisms  by which the materials deform.

Due to their synthesis and thermo-mechanical processing history, polycrystalline metals are generally crystallographically textured, and therefore their mechanical  and physical properties are often highly anisotropic (orientation dependent). The directionality of the mechanical properties must be taken into account when modeling for instance sheet metal forming operations. 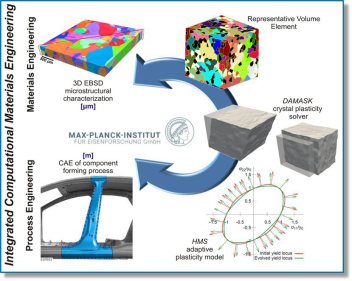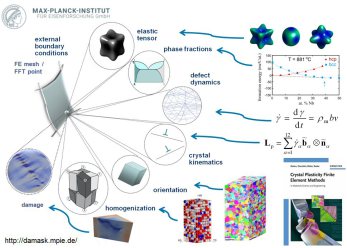The anisotropy induced by plastic strain during forming operations is usually relatively small compared to that induced by the preceding thermo-mechanical treatment and negligible for many applications. Crystal plasticity models such as DAMASK which use the crystallographic texture and the intrinsic single crystalline
anisotropy as input can accurately describe the anisotropic behavior of polycrystalline materials and naturally consider the stress and strain partitioning among different phases, grains, and subgrains. 

Starting with the first anisotropic yield function proposed by von Mises (1928), various yield functions have been introduced to describe the flow behavior of different materials. The quadratic anisotropic yield function developed by
Hill (1948) was often validated by numerous experiments and is usually quite well suited for homogeneous body centered cubic (bcc) materials, especially for
simpel ferritic steels (Hill, 1990). However, it can usually not accurately describe the yield behavior of more complex steels or of face centered cubic (fcc) metals, e.g., aluminum alloys (Hosford, 1988), as only higher order functions are then usually capable of predicting the rather angular form of yield surfaces. To overcome these limitations, Hill (1979) and Hosford (1985) proposed non-quadratic anisotropic yield functions. Later, Barlat and Lian, Barlat et al. (1991, 1997, 2003, 2005), Karafillis and Boyce (1993), and Banabic et al. (2003),  introduced further improved yield surafce formulations, where linear transformations of the stress tensor are used to describe the anisotropy (Barlat et al., 2007).

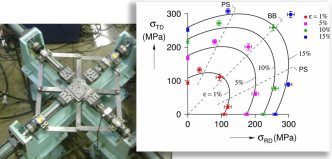
For yield surafce material models used in a commercial context, it is preferable that only a small set of simple and low-cost tests, e.g., uniaxial tensile tests, are necessary for calibration. The ability of advanced yield functions to describe the
mechanical anisotropy of various material classes, however, comes at the price of requiring many parameters. Improved flexibility and accuracy therefore makes the parameter identification process more challenging as more experimental results are needed. These experiments are expensive, time consuming, and sometimes very difficult to perform, e.g., when out-of-plane properties of sheet metals are required. Additionally, since no standards are defined for most of these experiments, evaluation of a parameter set requires an in-depth knowledge about the details of the fitting procedure that was employed to
retrieve it. In such situations it is less expensive to use crystal plasticity simulations for deriving the required parameters for the yield surface functions.

Polycrystal and poly-phase homogenization models can be used to examine the mechanical response of polycrystalline materials. Micromechanical models based on crystal plasticity theory play a significant role in understanding yielding and anisotropy of metals, as well as in evaluating yield surface models. The earliest of such approaches, proposed by Sachs (1929), uses an iso-stress approach and assumes the same resolved stress on the slip systems with the highest resolved shear stress in all grains within the polycrystalline aggregate. In contrast, the full-constraint (FC) model developed by Taylor (1938) is based
on the iso-strain assumption, i.e., all grains within an aggregate experience the same state of deformation. The FC TAYLOR model was elaborated further by Bishop and Hill (1951), and was used as the TAYLOR-BISHOP-HILL (TBH) model by many researchers to validate yield functions (Hosford, 1972; Barlat and Lian, 1989; Barlat et al., 1997) or to generate the analytical expressions for
plastic potentials and yield surfaces of anisotropic polycrystalline materials (Gambin, 1991; Van Houtte, 1994, 2001; Li et al., 2003; Van Houtte and Van Bael, 2004; Kowalczyk and Gambin, 2004; Van Houtte et al., 2009). It should be noted that the SACHS model satisfies the stress equilibrium condition across the grains but violates the compatibility condition between them, while, in contrast, the TBH model violates the stress equilibrium condition but satisfies the compatibility condition among differently oriented grains (Kocks, 1958). The deformation behavior of real polycrystals, where both, compatibility and
equilibrium are fulfilled, is in-between these two extremes (Sachtleber et al., 2002). The former model therefore sets the lower bound and the latter is the upper bound of the observed behavior.