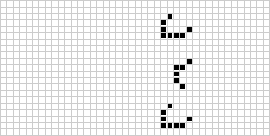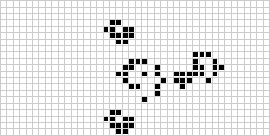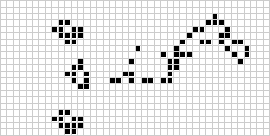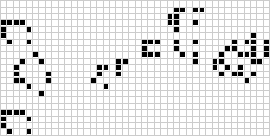
Cellular automaton simulations in materials science and microstructure prediction
Basic properties and features of cellular automata
Cellular automata are synchronous algorithms that describe the discrete spatial and temporal evolution of complex systems by applying local (or mesoscopic, mid-range)
deterministic or probabilistic transformation rules to lattice cells with local connectivity. Cellular automata are hence very well suited to describe complex topological microstructure
evolution phenomena, both in liquid, colloidal, and solid materials.
The concept of cellular automata was introduced in the late 1940's by von Neumann and Ulam for the simulation of self-reproducing Turing automata and population evolution.
In his early contributions von Neumann denoted these algorithms as cellular spaces. Other authors used notions like tessellation automata or iterative arrays. Early applications were particularly in
the fields of fluid dynamics, biological processes, and reaction-diffusion systems. During the last decade cellular automata gained momentum for the field of microstructure
simulation.
Cellular automata do not have restrictions in the type of elementary entities or rules they use. They can map such different situations as the distribution of the values of state variables in a
finite difference simulation, the colors in a blending algorithm, the elements of fuzzy sets, or growth and decay processes of cells. For instance, the Pascal triangle can be regarded as a
one--dimensional (1D) cellular automaton where the value of a lattice point of a regular triangular lattice is calculated through the summation of the two numbers above it. In this case the entities
of the automaton are integer numbers and the rule is a summation.
The space variable in cellular automata usually represents real space, but orientation space, momentum space, or wave vector space are used as well. Cellular automata can have arbitrary dimension.
The lattice of the automaton maps the elementary system entities that are regarded as relevant to the model. The individual lattice points can represent continuum volume units, atomic particles,
larger groups of atoms, cars, populations, lattice defects, or colors depending on the model. The state of each lattice point is characterized in terms of one or more generalized state variables.
These can be dimensionless numbers, particle densities, lattice defect quantities, crystal orientation, particle velocities, blood pressure, animal species or any other quantity the model requires.
The actual values of the state variables assume at each cell one out of a finite set of discrete states. The opening state of the automaton consists in the initial distribution of the values of the
state variables for a chosen lattice.
The dynamical evolution of the automaton takes place through the application of deterministic or probabilistic transformation rules that act on the state of each lattice point. These rules determine
the state of a cell as a function of its previous state and the state of its neighboring cells. The number of neighbor sites considered by the transformation (switching) rule when
calculating a state switch determines the range of the interaction and the local evolution of the automaton.
Cellular automata work in discrete time steps. After each time interval the values of the state variables are updated for all lattice points in synchrony. Owing to these features, cellular automata
provide a discrete method of simulating the evolution of complex dynamical systems which contain similar components on the basis of simple local interactions.
The cellular automaton method is, therefore, sometimes referred to as a counterpart to partial differential equations, which have the capability to describe dynamical systems in a continuous fashion.
The meaning of 'discrete' in this context is, that space, time, and properties of an automaton can assume only a finite, countable number of states.
The basic rational of cellular automata is not to try to describe the evolution of complex systems by a global viewpoint, i.e. by using averaging differential equations, but by simulating such
systems on the basis of the elementary dynamics of the interacting constituents following simple generic rules. In other words the cellular automaton approach pursues the goal to let the complexity
of dynamic systems emerge by the interaction of simple individuals following trivial rules.
Cellular automata fall into four classes of behavior. Class 1 cellular automata evolve for almost any initial configuration after a finite number of time steps to a homogeneous and unique state from which they do not evolve further. Cellular automata in this class exhibit the maximal possible order both at the global and local scale. The geometrical analogy for this class is a limit point in the corresponding phase space. Class 2 cellular automata create short period patterns that repeat periodically, typically recurring after small periods, or are stable. Local and global order is exhibited in such automata. Class 2 automata can be interpreted as filters, which derive the essence from discrete data sets for a given set of transformation rules. In phase space such systems form a limit cycle. Class 3 cellular automata lead from almost all possible initial states to aperiodic chaotic patterns. The statistical properties of these patterns and the statistical properties of the starting patterns are almost identical at least after a sufficient period of time. The patterns created by class 3 automata are usually self--similar fractal arrays. After many time steps, the statistical properties of these patterns are typically the same for almost all initial configurations. Geometrically class 3 automata form strange attractors. Class 3 is the most frequent type of cellular automata. Class 4 cellular automata yield stable, periodic, and propagating structures which can persist over arbitrary lengths of time. Some class 4 automata dissolve after a finite steps of time, i.e. the state of all cells becomes zero. In some class 4 a small set of stable periodic figures can occur (such as for instance in Conway's game of life). By properly arranging these propagating structures, final states with any cycle length may be obtained. Class 4 automata show a high degree of irreversibility in their time development. They usually reveal more complex behavior and very long transient lengths, having no direct analogue in the field of dynamical systems. The cellular automata in this class can exhibit significant local (not global) order.
Raabe Philosophical Magazine cellular au[...]
PDF-Dokument [8.6 MB]
Cellular automata in materials science: microstrcture simulation
One typical application of cellular automata for materials-related simulations consists in mapping the values of relevant state variables onto the points of a lattice and using the local finite
difference formulations of the partial differential equations of the underlying model as transformation rules. The particular versatility of cellular automata for microstructure simulations
especially in the fields of recrystallization, dendritic growth, grain growth, and phase transformation phenomena is due to its flexibility in considering a large variety of variables and
transformations.
Discrete microstructure simulations which track kinetics and energy in a local fashion are of interest for two reasons. First, it is desirable to understand the dynamics of microstructure evolution
on the basis of the interaction of large densities of lattice defects which are characterized by a wide spectrum of properties and interactions in heterogeneous materials. For instance, in the fields
of recrystallization and grain growth the influence of local grain boundary characteristics, local driving forces, and local texture on the final microstructure is of particular interest. Second,
from a practical point of view it is necessary to predict microstructure parameters such as grain size or texture which determine the mechanical and physical properties of real materials subjected to
industrial processes on a phenomenological though sound physical basis.
The strength of cellular automata is that they combine the simplicity and scalability of a switching model with the physical stringency of a boundary dynamics model.
Cellular automata can use atomic-scale or continuum-scale elements as underlying units. Since continuum formulations are not intrinsically scaled such automata must be physically calibrated by
transformation rules which reflect the characteristic length and time scales of the model.
If local transformations in the same model must account for different activation energies and real time scales (e.g. competing recrystallization and recovery phenomena, bulk diffusion and grain
boundary diffusion, different interface mobilities) it is required to achieve a correct common scaling of the system. This point is essential since the transformation behavior and the dynamical
evolution of microstructure-oriented cellular automaton models are governed by noncoupled Boolean routines rather than by exact local solutions of coupled differential equations.
The scaling problem becomes particularly important when simulating nonlinear systems (which applies for most microstructure-based cellular automata). During the simulation it can be useful to refine
or coarsen the scale according to the evolving kinetics (time re-scaling) and spatial resolution (space re-scaling) of the system.
Acta-Mater-2012-CA-austenite-to-ferrite.[...]
PDF-Dokument [2.9 MB]
Acta Materialia 52 (2004) 2653 CA polyme[...]
PDF-Dokument [680.2 KB]
Mater Sc Engin A 454–455 (2007) CA and F[...]
PDF-Dokument [1.1 MB]
overview-cellular-automata.pdf
PDF-Dokument [1.3 MB]
Further reading on cellular automata in materials science and engineering
pdfs of publications on Cellular Automata
D. Raabe: Phil. Mag. A, vol 79 (1999), No 10, 2339–2358
Introduction of a scaleable 3D cellular automaton with a probabilistic switching rule for the discrete mesoscale simulation of recrystallization phenomena
D. Raabe, R. Becker: Model. Sim. Mater. Sc. Engin. 8 (2000) 445-462
Coupling of a crystal plasticity finite element model with a probabilistic cellular automaton for simulating primary static recrystallization in aluminum
D. Raabe: Acta Mater. 48 (2000) 1617–1628
Scaling Monte Carlo Kinetics of the Potts model using rate theory
D. Raabe: Annual Review of Materials Research 32 (2002) p. 53-76
Cellular automata in materials science with particular reference to recrystallization simulation
D. Raabe: Acta Mater. 52 (2004) 2653-2664
Mesoscale simulation of spherulite growth during polymer crystallization by use of a cellular automaton
A. Godara, D. Raabe: Modelling Simul. Mater. Sci. Eng. 13 (2005) 733-751
Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton
D. Raabe, L. Hantcherli: Comput. Mater. Sc. 34 (2005) 299–313
2D cellular automaton simulation of the recrystallization texture of an IF sheet steel under consideration of Zener pinning
C. Zheng, D. Raabe, D. Li: Acta Materialia 60 (2012) 4768–4779
Prediction of post-dynamic austenite-to-ferrite transformation and reverse transformation in a low-carbon steel by cellular automaton modeling
The concurrent ferrite recrystallization and austenitic transformation during intercritical annealing of cold-rolled DP steels is investigated by cellular automaton (CA) modeling. The simulations prov
Acta-Materialia-2013-recrystallization a[...]
PDF-Dokument [966.7 KB]