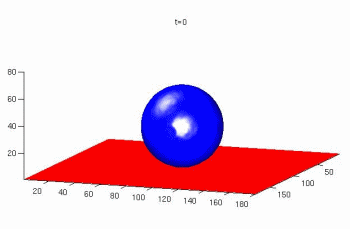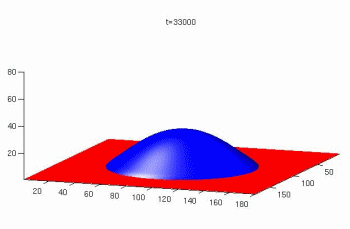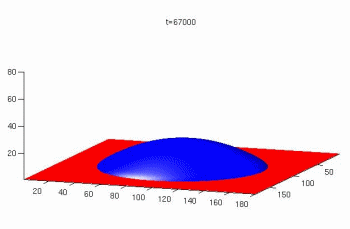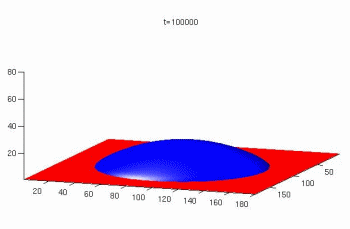
The Lattice Boltzmann method for simulations of microflows
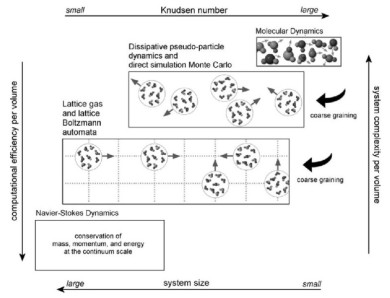
The lattice Boltzmann method is a powerful technique for the simulation of single and multi-phase flows in complex geometries. Owing to its excellent numerical stability and constitutive versatility it plays an essential role as a simulation tool for understanding advanced materials and processes. Unlike conventional Navier–Stokes solvers, lattice Boltzmann methods consider flows to be composed of a collection of pseudo-particles that are represented by a velocity distribution function. These fluid portions reside and interact on the nodes of a grid. System dynamics and complexity emerge by the repeated application of local rules for the motion, collision and redistribution of these coarse-grained droplets. The lattice Boltzmann method, therefore, is an ideal approach for mesoscale and scale-bridging simulations. It is capable to tackling particularly those problems which are ubiquitous characteristics of flows in the world of materials science and engineering, namely, flows under complicated geometrical boundary conditions, multi-scale flow phenomena, phase transformation in flows, complex solid–liquid interfaces, surface reactions in fluids, liquid–solid flows of colloidal suspensions and turbulence. Since the basic structure of the method is that of a synchronous automaton it is also an ideal platform for realizing combinations with related simulation techniques such as cellular automata or Potts models for crystal growth in a colloidal, soft matter, glassy, fluid, or gas environment.
This work is an overview of the lattice Boltzmann method (LBM) as a technique for the simulation of single and multi-phase flows in complex geometries. Owing to its excellent numerical stability and c
Modelling Simul. Mater. Sci. Eng. 12 (20[...]
PDF-Dokument [995.4 KB]
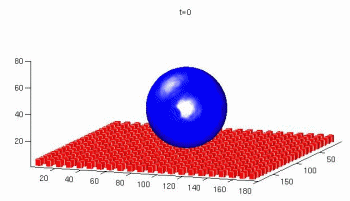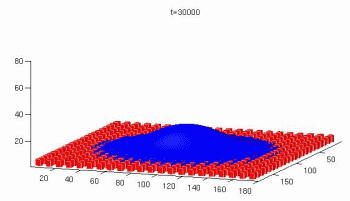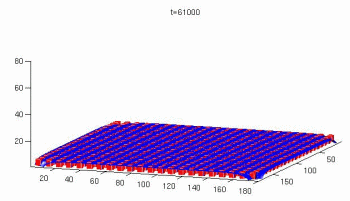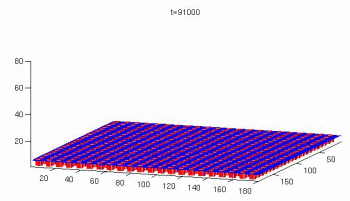
Effects of wall roughness/topography on flows in strongly confined (micro-)channels
are studied by means of lattice Boltzmann simulations. Whereas wall roughness in
macroscopic channels is considered
roughness-induced-instability.pdf
PDF-Dokument [731.8 KB]
Flow of driven amorphous solids does not proceed homogeneously, even if the
macroscopic stress is constant across the system. Via event-driven molecular dynamics simulations of a hard sphere glass, th
Phys-Rev-Let-Mandal_Heterogeneous_Shear_[...]
PDF-Dokument [355.3 KB]
Lattice Boltzmann Modeling of Advection-Diffusion-Reaction Equations: Pattern Formation Under Uniform Differential Advection
Ayodele-Lattice-Boltzmann-Commun. Comput[...]
PDF-Dokument [443.3 KB]
Acta_Materialia_2009_vol_57_page_1755_LB[...]
PDF-Dokument [1.2 MB]
Lattice Boltzmann modeling of dendritic growth in forced and natural convection
CAMWA_dendritic growth in forced and nat[...]
PDF-Dokument [1.4 MB]
transverse diffusive broadening PHYSICAL[...]
PDF-Dokument [348.7 KB]
Simulation of deformable particles immersed in a
fluid using a combined immersed boundary lattice Boltzmann finite element method
LBM deformable particles CAMWA 2011.pdf
PDF-Dokument [1.5 MB]