Cellular automaton simulation methods for recrystallization in metals and crystallization in polymers

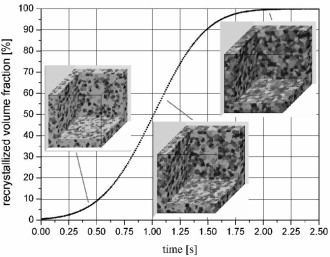
The paper is about cellular automaton models in materials science. It
gives an introduction to the fundamentals of cellular automata and reviews applications, particularly for those that predict recrystallization phenomena. Cellular automata for recrystallization are typically discrete in time, physical space, and orientation space and often use quantities such as dislocation density and crystal orientation as state variables. Cellular automata can be defined on a regular or nonregular two- or three-dimensional lattice considering the first, second, and third neighbor shell for the calculation of the local driving forces. The kinetic transformation rules are usually formulated to map a linearized symmetric rate equation for sharp grain boundary segment motion.
While deterministic cellular automata directly perform cell switches by sweeping the corresponding set of neighbor cells in accord with the underlying rate equation, probabilistic cellular automata calculate the switching probability of each lattice point and make the actual decision about a switching event by evaluating the local switching probability using a Monte Carlo step. Switches are in a cellular automaton algorithm generally performed as a function of the previous state of a lattice point and the state of the neighboring lattice points. The transformation rules can be scaled in terms of time and space using, for instance, the ratio of the local and the maximum possible grain boundary mobility, the local crystallographic texture, the ratio of the local and the maximum-occurring driving forces, or appropriate scaling measures derived from
a real initial specimen. The cell state update in a cellular automaton is made in synchrony for all cells. The review deals, in particular, with the prediction of the kinetics, microstructure, and texture of recrystallization. Couplings between cellular automata and crystal plasticity finite element models are also discussed.